Crystals with golden ratios - the full text

When Dan Shechtman recorded in his lab notebook the discovery for which he was awarded the 2011 Nobel Prize in Chemistry, he attached three question marks next to it

Figure 1. Daniel Shechtman's interference pattern had an axis of symmetry of order 10: rotating the image by a tenth of a complete circle (36 degrees) led to obtaining the same pattern.
When Daniel Shechtman recorded in his lab notebook the discovery for which he was awarded the Nobel Prize in Chemistry for 2011, he attached three question marks next to it. The atoms in the crystal placed before him yielded forbidden symmetry. The discovery was as impossible as a soccer ball, which is shaped like a ball, is made up of only hexagon shapes. Since that discovery, mosaics with fascinating patterns and the golden ratio, which until then had been known in the fields of mathematics and art, have helped scientists explain Shechtman's controversial observation.
"There is no such animal," said Daniel Shechtman to himself. "Such a creation is not possible." It was the morning of April 1982, 1. The substance he was examining, a mixture of iron and manganese, was strange in appearance, and therefore he approached the electron microscope in order to examine it at its atomic level. However, the image produced through the microscope was contrary to all logic: he saw before his eyes concentric circles (circles with a common center), each of which consists of ten bright points located at the same distance from each other (Figure XNUMX).
Shechtman quickly cooled the glowing metal fuse due to his assumption that a sudden change in temperature would lead to complete disorder in the atoms. But the pattern he saw told a completely different story: the atoms were arranged in a pattern that defied the laws of nature. Shechtman went back and counted the points again and again. Four or six points in the circle could be a possible find, but ten points is completely impossible. He made a note in his lab notebook: "10th order axis of symmetry???"

Peaks and valleys work together

In order to understand Shechtman's experiment and why he was so surprised, imagine in your mind the following classroom experiment: a physics teacher shines light through a perforated metal plate, what is known as a diffraction grating (Figure 2). When the light waves travel through the lattice, they are refracted in the same way as the waves of the sea passing through a gap in the breakwater in the harbor are refracted. On the other side of the lattice the waves spread out in a semi-circular pattern and intersect with other waves. Peaks and valleys of the waves amplify and weaken each other respectively. A pattern of lighted and darkened areas will appear on the monitor placed behind the probability grid - the probability pattern.
Daniel Shechtman received such a diffraction pattern (Figure 1) that morning in April 1982. However, his experiment was a little different: he used electrons instead of light, his lattice was composed of atoms cooled rapidly in a metal, and he conducted his experiment in three dimensions.
The diffraction pattern showed that the atoms within the metal were organized in an ordered crystal form. This finding itself was not unusual. Almost all solid substances, from ice to gold, consist of ordered crystals. However, the diffraction pattern of ten bright spots arranged in a circle was a finding he had not encountered before, despite his extensive experience using an electron microscope. Furthermore, this type of crystal is not included in the international tables of crystallography - the main crystal guide in the world of science. At that time, it was self-evident to science that a pattern with ten points in the shape of a circle was simply impossible.

A pattern that defies all logic

Inside the crystal, atoms are organized in repeating patterns, and depending on the chemical composition, they have different symmetries. In Figure 3a, it can be seen that each atom is surrounded by three identical atoms in the repeating pattern, obtaining symmetry of the 3rd order - that is, rotating the image by 120 degrees (360 divided by 3) will result in receiving the same image.
The same principle also applies for order 4 (Figure 3b) and order 6 (Figure 3c) symmetries. The pattern repeats itself and if you rotate the image by 90 (360 divided by 4) and 60 (360 divided by 6) degrees, respectively, the same patterns will be applied.

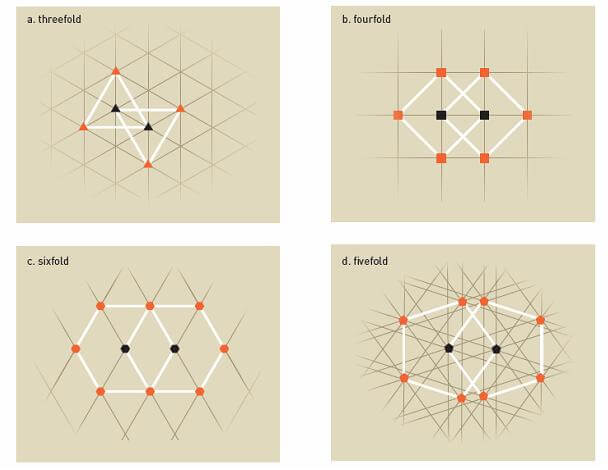
However, for the 5th order symmetry (Figure 3d), this is not possible, since the distances between certain atoms will be shorter than between others. The pattern does not repeat itself, a fact that was sufficient proof for scientists that it is not possible to obtain 5th order symmetry in crystals. The same is true for symmetry of order 7 or higher.

Nevertheless, Schechtman could rotate his probability pattern a tenth of a circle (36 degrees) and still get the same pattern. Therefore, he looked at 10th order symmetry, which at the time was considered impossible. Therefore, there is no wonder that he marked no less than three question marks in his laboratory notebook.

Error in the textbooks

Daniel Schechtman looked out of his office toward the hallway at the US National Institute of Standards and Technology (NIST), and wanted to find someone with whom he could share the discovery. However, the corridor was empty, so he returned to his microscope to conduct further experiments on the particular crystal. Among other experiments, he checked again if he might have obtained twin crystals: two crystals growing from a common boundary lead to strange diffraction patterns. However, he found no sign that he had actually observed twin crystals.

In addition to this, he rotated the crystal inside the electron microscope in order to check how much rotation he could activate until the 10th order diffraction pattern appeared again. This experiment showed that the crystal itself does not have 10th order symmetry similar to the probability pattern, however it is based on 5th order symmetry, which was just as improbable (at the same time) as 10th order symmetry. Daniel Shechtman came to the conclusion that the scientific community must have been wrong in its assumptions.

When Schechtman told other scientists about his discovery, he was faced with complete doubt about the reliability of his findings on their part, and some of his colleagues even began to mock him for it. Many of them claimed that what he saw was actually a twin crystal. The director of the laboratory gave him a textbook of crystallography and suggested that he should read it. Schechtman, of course, already knew about everything that was said about him, but he trusted his experiments more than the textbooks. All this turmoil led his manager, eventually, to ask him to leave his research group, as Schechtman himself later recalled. The situation has become too awkward.

Struggle with established knowledge
Daniel Shechtman received his doctorate from the Technion - the Israel Institute of Technology, and in 1983 he managed to interest his colleague Ilan Belch in his strange research findings. Together they tried to interpret the probability pattern and translate it into an atomic array of a crystal. They submitted their article to the scientific journal Journal of Applied Physics in the summer of 1984. But the article was returned, ostensibly due to problems with the mail, but in fact the editor rejected the article immediately.

At this point, Shechtman asked the researcher John Cahn, a famous physicist who persuaded him to come to the institutes in the USA in the first place, if he was willing to review the information he had. The researcher, who was usually too busy to carry out such a task, examined the findings and contacted a French crystal expert (Denis Gratias) to see if Schechtman might have missed something. However, according to the expert, Shechtman's experiments were reliable. He claimed that if he had been required to conduct the experiments himself, he would have done exactly the same as Shechtman.
In November 1984, together with the three researchers who helped him and examined his findings again, Shechtman was finally able to publish his findings in the scientific journal Physical Review Letters. The article caused an uproar among crystallographers. He questioned the fundamental truths of their field of science: that all crystals are composed of repeating periodic patterns.

Remove the blindfold

The discovery now reached a wider audience, and Daniel Shechtman became the target of even greater criticism. On the other hand, at the same time, crystallographers from around the world experienced a moment of déjà vu. Many of them obtained similar diffraction patterns during the tests of other materials, but they interpreted them as evidence of twin crystals. Now they began digging under their old pages to find old lab notebooks and soon other crystals began to appear with patterns that were considered impossible at the time, crystals with 8th and even 12th order symmetry.

When Schechtman published his discovery, he still did not have a precise understanding of the detailed internal structure of the strange crystal he was studying. In the end it was proved that its symmetry is of order 5. But how are the atoms arranged? The answer to this question will come from a completely unexpected place: mathematical challenges with mosaics.

The mosaics of explanation

Mathematicians like to challenge themselves with additions and logic problems. During the sixties they began to ponder whether it was possible to create a mosaic with a limited number of tiles (building blocks) so that the pattern would never repeat itself, to create what is known as an aperiodic mosaic. The first successful attempt was reported in 1966 by an American mathematician. For this he needed more than twenty thousand different tiles - a finding that was very far from satisfying the mathematicians' fondness for brevity. Once more and more people took on the challenge, the number of pavers required shrank and went steadily.
Eventually, in the mid-seventies, a British professor of mathematics, Roger Penrose, provided a very clever solution to the problem. He was able to create non-cyclic mosaics by using only two different tiles, for example - a narrow rhombus and a wide rhombus (Figure 4:1).

The Penrose mosaics have inspired the scientific community in a number of different ways. Among other fields, his findings have been used since the discovery to analyze Islamic art patterns from the Middle Ages, and it soon became clear that the Arab artists created non-cyclic mosaics from five unique tiles as early as the 13th century. Such mosaics decorate the "Alhambra" palace in Spain, as well as the gates and domes of the "Sharin" mosque in Iran.

The crystallographer Alan Mackay used the Penrose mosaic in a different way. He was curious whether atoms, the building blocks of matter as it is, might form non-periodic patterns similar to mosaics. He conducted an experiment in which he converted circles, representing atoms, at the intersection points of the Penrose mosaic (Figure 4:2). In the next step, he used this pattern as a diffraction lattice in order to check what the diffraction patterns could be obtained. The result was 10 order symmetry - ten illuminated points in the shape of a circle.
The link between McKay's model and Shechtman's probability model was eventually made by physicists Paul Steinhardt and Dov Levin. Before the article appeared in the scientific journal Physical Review Letters, the editor sent it to other scientists for review. During this process, the physicist Steinhardt got a chance to read it. He was already familiar with McKay's model and understood that the theoretical 10th order symmetry was already alive and breathing in Shechtman's laboratory.

On Christmas Eve 1984, just five weeks after Shechtman's paper appeared, the two physicists published a paper in which they described quasicrystals and their non-periodic mosaics. Quasi-crystals were first named in this article.

The golden ratio - the answer

A fascinating aspect of both quasi-crystals and non-periodic mosaics is the golden ratio (Wikipedia term) that exists in mathematics and art, the mathematical constant tau (τ) that appears repeatedly). For example, the ratio between the thin and thick rhombuses in Penrose's mosaic is tau. Similarly, the ratio of distances between atoms in quasi-crystals is always a tau constant.

The mathematical constant tau is described by a sequence of numbers that the 13th century Italian mathematician Fibonacci discovered from a hypothetical rabbit breeding experiment. This is a very familiar sequence of numbers where each number is the sum of the two preceding numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. If you divide the high numbers of the Fibonacci sequence by the number before them - for example, 144/89 - you get a number very close to the golden ratio.

• The original news in English (there you can also find Figure 4 that was not uploaded here)
• Detailed scientific background
• For further reading and important links