A possible proof of the existence of twin prime infinities was presented

The proof of the question, which is one of the most famous unsolved questions in number theory, was released to the general public at the end of May and is due to be reviewed by a panel of experts

Yanon Kostica

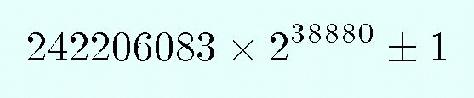
Direct link to this page: https://www.hayadan.org.il/primetwin.html

Number theory poses a wide variety of questions that are very easy to formulate, but their solution remains unknown to this day despite great efforts invested in the matter. Many of those problems involve prime numbers, which are numbers divisible by only one and by themselves, which are widely used today in most modern encryption methods.
One of these problems is called the Twin Primes problem. Twin primes are a pair of prime numbers whose difference is 2, such as (3,5), (41,43). While it has been proven that there are an infinite number of prime numbers, the question of whether there are an infinite number of twin primes has remained unsolved since the early 20th century, although most mathematicians believe that the claim is indeed true. The problem is considered one of the central problems in number theory that have not yet been solved.
This month published R. P. Arenstorf (RF Arenstorf) of Vanderbilt University in Tennessee A 38-page paper presenting a possible proof of the claim using methods from classical analysis of number theory. The article is on arxiv.org, and is accessible to the general public.
At the opening ceremony of the Hebrew University, held on April 1, 1925 on Mount Scopus, the German-Jewish mathematician Edmund Landau from the University of Göttingen gave a lecture on "Solved and Obscure Questions in Elementary Number Theory". One of the first questions he presented was the problem of the twin primordials: "This is what Satan knew. I would like to say that, apart from the Lord of the world, there is no one who knows this, not even my friend Hardy at Oxford who, among all my colleagues, is the most profound researcher in this field," he said regarding a possible answer.
Much research on the subject has been conducted since then, in many and varied directions, but no possible proof of the question has been found to date. In 1919, the Norwegian mathematician Viggo Brun proved that the sum of the inverses of all the twin primes (ie the column (1/3+1/5)+(1/5+1/7)+..) converges to a final value that was later called " Constant Baron" and its value ..1.9021 The convergence of the column led to many hopes being dashed, because if the column had not converged to a finite value, then there would certainly exist an infinite number of twin primes.
At the beginning of the century it was known that the column converges, but the convergence value was not known with sufficient accuracy, since for this purpose calculations involving tens of billions of twin primes must be made. Only in 1974 was a satisfactory calculation made for Baron's constant, and two years later the value was discovered with even higher accuracy after a calculation of about one hundred billion twin primes (!).
Thomas Nicely (Thomas Nicely) from the University of Lynchburg in Virginia approached in 1994 to verify the value of Barron's constant and even calculate it with higher accuracy by calculating trillions of twin primes. By the way, Nicely discovered that during the calculation the result is getting more and more wrong. A careful examination of the matter revealed that the malfunction was due to a defect in Intel's Pentium processor, which was released on the market that year. This flaw later became known as the well-known "Pentium bug", which led to the collapse of Intel shares and a severe crisis of confidence with consumers.
In recent years, the computer has been harnessed to find twin primes with many digits. For example, all the small twin primes were calculated from ten thousand trillion (one followed by 16 zeros) by Patrick Frey at the Polytechnic Institute in the State of New York. The largest twin primes known today have 32,220 decimal digits.
A different approach was taken by P. Kelly and Terry Pilling from the University of North Dakota, who focused on the scattering of the twin primes on the scale of the primes only, and not on the scale of the natural numbers as was done until then. They tested how "single" primes separate each successive pair of twin primes, i.e. between (17,19) and (29,31) a single single prime separator (23), and between (5,7) and (11,13) ) does not separate an initial nose. The number of separating primes is called Prime Separation. Based on an analysis of twin primes smaller than four billion, Kelly and Pilling determined that for a sufficiently wide range of natural numbers, the relative frequency of twin primes (relative to prime numbers) is given by a logarithmic ratio that is astonishing in its simplicity.
The published proof is now being examined by a team of experts who will determine whether it actually proves the claim. The test will last several months at most, and at the end we will know whether one of the biggest open questions in number theory has been solved.
In addition to twin primes, there are also "cousin primes" which are a pair of primes with a difference of 4 (for example 19,23), and sexy primes (from the word six in Latin, Sexy Primes) whose difference value is 6, such as (7,13) .

links:

The possible proof of the problem of the twin primordials

More on twin primes
An article in Galileo about the Pentium failure and how it was discovered
The math genius

https://www.hayadan.org.il/BuildaGate4/general2/data_card.php?Cat=~~~867973294~~~133&SiteName=hayadan