In an article published in "Science" three researchers from the Technion write that experiments in optics shed light on the conduction properties of semi-crystals
Three researchers from the Technion, doctoral student Liad Levy, post-doctoral student Michael Rechtsman and research professor Moti Segev, were able to show that adding disorder to quasi-periodic structures increases the conduction properties of materials, and even explain the physical mechanism behind this phenomenon. All of this is contrary to the popular opinion that the existence of disorder within crystals suppresses the conduction property of materials and does not increase it. This is what the prestigious scientific journal "Science" reveals.
The question of the conduction of particles (electrons) in quasi-crystals is a question that has occupied the scientific community since the discoveries of these materials until today. Technion researchers used an optical system to build a photonic quasi-crystal, added disorder to it and sent a beam of light into it to follow the propagation of light within the quasi-crystal. The idea for this specific study was first brought up by three other researchers in Professor Moti Segev's research group: Barak Friedman, Tal Schwartz and Ofer Menela - towards the end of their doctorates (under the guidance of Moti Segev) about three years ago, but an essential part of the problem "exploded" only about a year ago By Liad Levy, Michael Rechtsman and Moti Segev.
The researchers explain that the way electrons move in different materials determines their electrical conduction properties, while the way photons (particles of light) move in different materials determines the properties of the "transmission of light" through these materials. But it is natural that the conduction mechanisms of particles and light in different materials will be a central topic of research in physics, and indeed the first fiscal models for the conduction of light in different materials were already proposed about 1000 years ago!
Claudius Ptolemy - a Roman citizen who lived in Alexandria, Egypt - was the first to find a mathematical relationship between the angles of refraction of light rays passing through different materials when the angles are small. Only 600 years later (1621) the mathematician Wilburd Snell found the exact relationship between the angles of refraction of light for any angle (Snell's law).
As for the conduction of electrons, the first model to describe the conduction of electrons in metals was proposed at the beginning of the last century (in 1900) by the physicist Paul Drode. Drode assumed that the electrons are "small balls" that during their movement often collide with the atoms of the material - "big balls fixed in their place" - and perform a random movement inside it called a "drunk motion".
"Although these models - for electrons and/or photons - corresponded to a significant part of the experiments conducted with light waves and electric current conduction experiments in conductors, it is clear to us today that the picture is much more complex and that the basic assumptions of Drode and Snell's type are insufficient", say the Technion researchers. In 1801, the physicist Thomas Young showed that light maintains the properties of waves, by a simple experimental set-up of interference from two slits, in which points of darkness were obtained on a screen as a result of destructive interference between two different light sources (evidence of the wave nature of light). In 1961, an identical experiment was performed with an electron beam that gave the same result (and confirmed a prediction of quantum theory) - evidence of the wave nature of particles. In light of these discoveries, it is clear that the basic assumptions used by physicists and mathematicians such as Snell and Drode were inadequate: if electrons (and/or photons - the particles of light) have wave properties, then the particles are capable of bypassing "obstacles" and even entanglement as waves in the sea do. Therefore, Droda's central assumption - that the electron is a particle ("kind of like a small billiard ball") moving in straight lines - is incorrect.
Answers to the complete description (almost...) of the movement of particles and light in matter began to appear after the birth and establishment of the electromagnetic theory (Maxwell's complete equations) and the quantum theory (Schrödinger's equation).
The first shot to understand the conduction properties of waves (including interference phenomena) was fired by the Jewish physicist, Nobel laureate, Felix Bloch (1928). In Bloch's time, the scientific community without exception believed that all solids in nature are made of atoms/molecules that are placed cyclically next to each other and form a periodic and ordered crystal. This is why Bloch did not understand how electrons behave in such structures within the framework of quantum theory. In his doctoral thesis, Bloch solved the Schrödinger equation for electrons moving in periodic structures while treating the electrons as waves and calculating the interference created as a result of the periodic structure. Bloch's calculation laid the foundations for understanding the movement of electrons in materials in nature. However, Bloch's description was not complete either, and even though it suited many experiments - it failed to explain many other phenomena.
"Two key assumptions were not taken into account," the researchers explain. "First, Bloch's theory is based on a perfect cyclical structure. However, such a structure exists only in theory: in every system in nature there is also disorder to a certain extent. Therefore, in order to describe conduction in different materials, we must assume that although solids in nature are cyclic structures at their core, there is a certain degree of disorder in them - holes, particles that are not in their place, and even different particles scattered randomly and at low density within the cyclic structure. In 1958, an American physicist named Philip Anderson stunned the scientific community when he published the first solution to the question of wave propagation (any waves, including particles behaving as waves) in periodic structures (crystals) that also have a certain degree of disorder. Contrary to the popular opinion until then, which held that disorder indeed interferes with conduction but does not eliminate it, Anderson showed that the addition of disorder to a periodic structure in which the particles (such as electrons) move, even to a small degree, can completely eliminate the material's conduction property. Anderson showed that under certain conditions disorder places the particles (for example, electrons carrying the electric current) within a bounded region from which they cannot escape. This discovery has significance in many physical systems. For example, in such a situation, in materials with electrical conduction properties, a current cannot develop, so the material loses its electrical conduction property and behaves as an insulator.
This phenomenon is called "Anderson Localization" - after the name of the discoverer of the phenomenon.
Anderson was able to explain many experiments that were not understood before his work, and many experiments after it supported the correctness of his solutions and the predictions they provided. For this, Anderson received the Nobel Prize in Physics in 1977. However, in fact the first experiment that would reproduce the exact conditions for which Anderson solved the question of conduction in periodic structures in the presence of disorder was performed only in 2007 in the research group of Professor Moti Segev at the Technion. In their doctoral thesis, Dr. Tal Schwartz and Dr. Guy Bartel, in collaboration with Professor Shmuel Fishman of the Technion and Moti Segev himself, succeeded in putting together an optical system that was able to realize the conditions from Anderson's article from 1958 and for the first time directly show in an experiment the phenomenon of Anderson localization.
"Secondly", say the researchers, "the assumption that all solids in nature are basically cyclic structures is not correct. While the first assumption (that every system in nature has a certain degree of disorder) is logical, the existence of solids in nature that are not fundamentally cyclic structures - but also do not have a random structure - is an assumption that is not expected at all.
Until the 1982s, all crystals that were studied were composed of a basic structure ("unit cell") that repeats itself cyclically and forms a periodic crystal. However, in 1984, research professor Dan Shechtman from the Technion discovered experimental evidence for the existence of quasi-periodic solid materials: materials in which the atoms/molecules are not arranged in a periodic (crystalline) manner on the one hand, but are also not randomly distributed on the other hand. These are ordered materials that are not cyclic: they do not have a "unit cell" that repeats itself cyclically (as there is in crystals), but nevertheless they have order because similar patterns can be found in their structure at a sufficiently large distance from each other. These materials are called quasi-crystals (semi-crystals). This discovery rocked the scientific world until another researcher named Dov Levin (today also a professor at the Technion) and his doctoral supervisor, Professor Paul Steinhardt, proposed (XNUMX) the theoretical model that explained the existence of the quasi-periodic materials that Professor Shechtman saw in the laboratory. Professors Levin and Steinhardt even coined the term - quasi-crystal".
For this discovery, Professor Shechtman won the prestigious Wolf Prize, and Professors Levin and Steinhardt won the Buckley Prize last year (and of course, Professor Segev and his research team hope that Shechtman, Levin and Steinhardt will win the Nobel Prize for the discovery of quasi-crystals).
As mentioned, Technion researchers Liad Levy, Dr. Michael Rechtsman and research professor Moti Segev used an optical system to build a photonic quasi-crystal, added disorder to it and sent light beams into it to follow the propagation of light within the quasi-crystal.
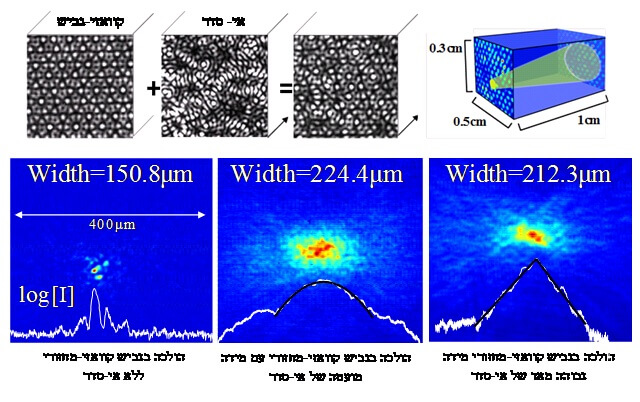
The following figures describe the main components of the experimental system and the results. In the upper part on the left side you can see the quasi-periodic crystal. At first glance, the pattern appears to be orderly and cyclical, but a closer look at the details in the image will reveal that there is no real cycle (there is no repeating "unit cell"). A pattern of "disorder" was added on top of this structure - the structure is messy - and the quasi-periodic crystal pattern was obtained with the addition of disorder. Into this pattern, a green beam of light is sent (upper part on the right side) which spreads inside it along 1 centimeter. The light beam sent into the medium consists of a very large number of photons that moved under the influence of the quasi-crystal in the presence of disorder. All the photons were launched from the same point (the center of the entrance lobe of the crystal) and after moving in the crystal, the photons were dispersed and a picture of their dispersion was taken by the camera. The above experiment was performed for a clean quasi-crystal (bottom left side) and for cases in which an increasing amount of disorder was added to it, until the remnants of the quasi-periodic structure were completely erased (bottom right side). It can be clearly seen how for the addition of a small amount of disorder (bottom middle part) the photons scattered to greater distances than the case where there is no disorder at all (bottom left side) - direct evidence that adding disorder to the quasi-periodic structure increases the the conduction feature.
The conclusions arising from this study have significant implications for the study of the conduction of both electrons in solids and for the study of the passage of light rays (electro-magnetic waves) through different materials. The elegant system built at the Technion opens up a horizon for further experiments. For example, so far we have been talking about structures fixed in time. It would be natural to ask what would happen to the movement of the particles if we add to the above structure a disorder that varies randomly even in time (random vibration)? After all, that's how it is in nature. Will changing the average size in the disorder pattern and/or the crystal change the results qualitatively? And if so how? This research does indeed answer a number of basic questions in science, but at the same time it opens up new questions and avenues of thought.
