Adolf Cutla believed that he was able to fit human beings into the same rigid framework that statistics had placed. "The coincidences," claimed Katala, "is just a veil that covers our ignorance."
For most of us, the people who only know the numbers and equations from boring lessons at school, this whole subject seems technical, boring and tedious - but any mathematician will tell you that mathematics is beautiful. It has an incredible elegance that is revealed mainly when you discover how much it is able to tie together natural phenomena that, on the face of it, seem completely unrelated to each other. The following story will demonstrate this elegance.
Adolphe-Jacques Quetelet (Quetelet) was born in the Belgian city of Ghent in 1796. He was a real man of letters: he wrote poetry, composed plays, translated books and also taught mathematics, physics and astronomy. He was a successful scientist, and the first to receive the title of 'Doctor of Science' from the University of Ghent.
In 1823 Catella was sent to Paris. The original purpose of the visit was to specialize in astronomy, but in France Catella met one of the greatest mathematicians of his generation - Pierre-Simon Laplace. It was a fateful meeting for Catella, as Laplace ignited in him a great love for statistics.
Statistics was a young and undeveloped field in those days, but the mathematicians who dealt with this subject had already managed to discover some intriguing facts.
Suppose, for example, that we measure the temperature of a bucket of boiling water using a thermometer. The thermometer is not perfect, so every time we put it in the bucket, we will get a different result. The changes will be tiny - fractions of a degree here or there: in one measurement we read 100.5 degrees, in the next measurement maybe 99.5 degrees.
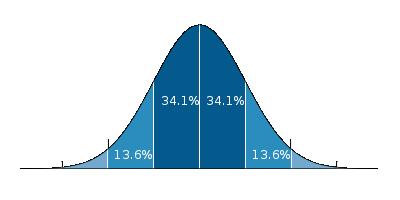
To be sure of our measurement result, we will perform a thousand different measurements and record the results in a graph: the horizontal axis in the graph will be the measured temperature and the vertical axis - how many times we got the same measurement.
The graph we will get will be bell-shaped: a high central area and margins that gradually get smaller. There will be a lot of measurements that move around the hundred degree point, and a few measurements that get further and further away from it - for example, ten measurements of 101 degrees, 5 measurements of 102 degrees and only 3 measurements of 104 degrees.
Mathematicians encountered this bell graph in many different experiments in physics. Almost every time a measurement was repeated over and over again, for example - measuring speed, electric current, length, width and what not - the result was a bell curve. In fact, so many experiments and measurements produced the same bell shape that it was given the name 'normal distribution': this is how nature behaves normally.
But physics is one thing, and humans are another. We are not a bucket of water with one temperature - we are different from each other. Each of us looks different: tall, short, thin, fat, bald, hairy and much more. The differences between humans, it seems, are completely random.
Adolf Cutla believed that he was able to fit human beings into the same rigid framework that statistics had placed. "The coincidences," claimed Katala, "is just a veil that covers our ignorance."
To prove his point, Catella measured the height of one hundred thousand recruits in the French army, and plotted the results on a graph. The height of most of the soldiers hovers around some certain value - for example, one meter and seventy centimeters - and as you move away from that value, the number of soldiers decreases. Only a small part of them rises to a height of one meter ninety or one meter fifty. If this description sounds familiar to you, you're right: the graph that received Katla had the shape of a...bell.
Hence, human height also obeys the same 'normal' statistical distribution of temperature measurements. Cutla found a certain order in a human trait that on the face of it is completely random. Cutla also measured the chest circumference of six thousand Scottish soldiers, and again got the same normal distribution.
Where is the connection between the behavior of a thermometer in a bucket of boiling water, and the height of French soldiers? On the face of it, these are completely different phenomena. Catella tried to solve this dilemma with an original explanation: he argued that nature was trying to create a human being (in this case, a French soldier) of an 'ideal' height. But nature misses. Instead of a soldier of the ideal height, he produces a 'wrong' soldier, of a different height than desired. The accumulation of these errors creates the bell curve, the same bell curve that also creates the temperature measurement errors in the bucket.
To modern eyes, it's easy to see that Killa is completely wrong. Nature doesn't try to 'create' anything, and if it was already trying to create something perfect - it certainly couldn't be a French soldier.
To complicate matters further, Katala decided to measure completely different things. For example, the suicide rate in a certain city, or the severity of crime by year, or the distribution of the age of marriage. Even there, he discovered, the graph looked exactly the same: a normal distribution.
The significance of this finding is nothing less than amazing. The same mathematical law, the same 'equation' if you will, that describes phenomena in the world of physics and astronomy - also describes phenomena that are completely non-physical, such as the age of marriage in Belgium and France. There is a deep and hidden connection between two fields that seem completely different on the surface, and this connection is mathematical. What is the meaning of this finding - and many like it - on our world view? Is mathematics a kind of canvas on which our reality is painted, a canvas that serves as a common background for every phenomenon we encounter? This is a question that has fascinated philosophers of mathematics for thousands of years, and will probably continue to do so for the foreseeable future.
[Catala's story is taken from the book 'Is God a Mathematician', by Mario Livio. Ran Levy is a popular science writer and hosts the podcast 'Making History!' About science, technology and history. www.ranlevi.co.il]

41 תגובות
I would like to prove that the normal distribution is genetic. Are there other phenomena other than the thermometer phenomenon that undermine this decision?
R.H.:
It just seems implausible to me that people's height is a sum (or average) of lots of independent variables and a distribution value.
What's more, the claim is not only about height but about almost everything and height was just an example.
Is it possible that almost everything is a sum of independent variables and the value of a distribution?
God,
You nicely demonstrate here the mechanism for my claim that a phenomenon consisting of several independent parameters will often show a normal distribution even if each parameter has only two values (as in your example one meter and two meters).
I don't understand why you think there is no normal distribution of people's height?
Rah and Lisa:
A distribution is indeed called normal because it is normal.
That still doesn't mean it has to be exactly the bell shape described by a particular function.
As a principle - it is not obvious that there will be any behavior that can be characterized as "normal".
The central limit theorem is an important theorem that says that when there are many lotteries with the same distribution, then the average of their results tends to a normal distribution (in its mathematical definition) as the number of lotteries increases.
This is a beautiful and important statement and it really explains why - if we take samples of very many people and measure the average height - and repeat the process many times - the different averages will be distributed over a curve approaching a normal distribution - as the size of the samples increases.
However - this will not make the curve of the distribution of people's heights look like a normal distribution!
For the sake of demonstration - suppose an imaginary world in which there are only two possible heights of a person - one meter and two meters with equal probabilities.
If you take a sample of a hundred people and calculate their average height you will get a number between 1 and 2.
If you take a thousand such samples and calculate their averages, these averages will spread over a bell curve close to the normal distribution.
(Actually, another thing will happen - the larger the samples are, this distribution will change because its variance will decrease and a relatively larger proportion of them will be concentrated around the average height, which is 1.5 meters in this example. This decrease in variance makes the continuation of the curve to minus infinity less and less relevant).
On the other hand - if you take those hundred thousand people - their heights will not be distributed on any bell curve!
Some of them will still be one meter high and some two meters high. Most likely these parts will be quite similar in the number of people in them. It is certain that no one will be found whose height is 1.5 meters, even though in the distribution of the averages we did, 1.5 was actually the average height with the highest probability.
The story with the dice is similar.
If you take a thousand samples of 100 rolls of a pair of dice - the averages of these samples will be spread over a curve that resembles a normal distribution.
If you take one sample of 100,000 tosses - it is likely that the results will be spread over a triangle.
Therefore - a normal distribution of throwing a pair of dice does not exist.
That's why - a normal distribution of people's heights is surprising (if it exists, but - in my opinion, it doesn't really exist either and, as with the measurements of many natural phenomena, it's only a convenient approximation. The intuitive explanation that this is a good approximation is based on the assumption that the height of each person is actually an average of A lot of lotteries with more or less the same distribution - something that can be justified if there are - let's say - 100 genes, each of which has many potential alleles and all genes have a similar effect on height)
R.H.:
I agree that roughly one could think that when examining phenomena in nature, one could intuitively think that certain values would be very common and others less so. But this is not enough to describe a normal distribution.
Regarding people's weight or eye color - I personally see no a priori reason to assume that these phenomena will be normally distributed (but in practice it turns out that many phenomena are indeed distributed that way).
What are the random variables whose sum determines a person's weight or height?
Lisa,
A normal distribution is not something mysterious. Many times an explanation can be found for it. For example, when there is a phenomenon that results from a combination of several independent factors, as a result of the combinations, a normal distribution will be obtained. For example sum of dice. Another example is the weight of people that is normally distributed. At the extremes there will be those who for genetic reasons + lack of food will be super thin and on the other side those who for genetic and behavioral reasons of overeating will be super fat. Everyone else will be in the middle. What is mysterious here?
Poor color or height are caused by several genes, so different combinations of them will result in different shapes. Only a very rare shroff will result in a height of over two meters or under a meter (in an adult) so again there is no wonder or mystery here.
R.H.:
This is also a way of looking at things, but I look at things like this:
There are many phenomena in nature that are distributed according to a certain distribution - this is one thing that is surprising in itself.
Now after they discovered this surprising discovery, they decided to call this distribution a normal distribution, because indeed it turns out that it is a very common distribution (but there are many phenomena that are not normally distributed).
The second surprising thing is not directly related to phenomena observed in nature but to the virtual world of mathematics. This is the central limit theorem and it says the following:
Take almost any distribution you like (even by scribbling a distribution on a page) and now start sampling samples from the distribution and sum them. The sum is a random variable in itself and it tends to a distribution, which happens to be called normal, the more samples we take.
The mathematical theorem is sometimes used as an explanation for the "normality" of the distribution and the fact that it is very common in nature.
Lisa,
I'm probably missing something here. A normal distribution is called normal because a lot of phenomena behave according to it and it is normal. So what is surprising about normal? Usually the abnormal is surprising.
R.H.:
What amazes me (at least to me) is that this does not at all depend on the distribution of the random variables that are summed up (to the extent of distributions with a duration or variation that is not finite).
It should be noted that the distribution of the sum aspires exactly to a normal distribution and not just to something that generally resembles a bell.
Lisa, why is this amazing? If there are several parameters that do not depend on each other and create a measurement phenomenon, it is assumed that this is what you will get.
Triangle because there are few values and it's an approximation, do the same with infinite cubes and you'll get your bell. Any calculation of probabilities is based on as many trials as possible. Flip a coin 3 times and you won't be able to conclude anything about the probability of getting a tree.
Of course, a triangle is also a "type of" bell.
That's why the question actually arises - what do you want to call a bell.
In general, it is possible to describe variables that are distributed in a way that does not even give a symmetrical shape.
R.H.:
I assume you mean the central limit theorem mentioned here. If we throw it into the example of the dice you gave, it says that the sum of the numbers is indeed a variable whose distribution will approach a normal distribution the more dice we take.
What is amazing about the theorem is that it is valid for almost any distribution of the variables that are summed (in the case of the cubes it was a uniform distribution over the values of the cube)
This fact is sometimes used as an explanation for the widespread presence of the distribution in various phenomena in nature. It is customary to assume, for example, that noise in measurements is normally distributed, and the explanation given is that the noise is the sum of many smaller factors.
This is not always justified, but there is also an engineering reason for this assumption, which is that the normal distribution of noise greatly simplifies the mathematical modeling of phenomena.
R.H.:
No.
If you draw yourself a 7x7 table in which the top row will represent (starting from the second column from the right) the result of cube A and the right column will represent (starting from the second row from the top) the result of cube B, you will be able to fill the table slots with the amount obtained by throwing represented by the combination of the row and the column.
The probability of each slot in the table is 36 / 1.
Therefore 2 is obtained with probability 36 / 1
3 is obtained with probability 36 / 2
4 is obtained with probability 36 / 3
5 is obtained with probability 36 / 4
6 is obtained with probability 36 / 5
7 is obtained with probability 36 / 6
8 is obtained with probability 36 / 5
9 is obtained with probability 36 / 4
10 is obtained with probability 36 / 3
11 is obtained with probability 36 / 2
12 is obtained with probability 36 / 1
If you draw the graph you will get a triangle
You are the mathematician. It seems to me that it is possible to prove that any phenomenon consisting of several parameters will behave in the shape of a bell.
For example, one cube will show an equal spread for all values, but two cubes will show a bell distribution with 7 in the center and 12 and 2 on the sides. Am I right?
R.H.:
You are not surprised that you did not "get to the top of the article".
As I said - all the amazement expressed in the article is about the mathematical similarity between the unrelated phenomena.
As I explained - the astonishment is not really justified because this mathematical similarity does not really exist and the mathematical description of the bell curve is not an accurate description of reality but only a convenient approximation.
You see in "bell" only a general description of the appearance of the curve, so I'm not surprised that you're not surprised 🙂
After all, all the astonishment (which in my opinion is not justified) stems from attributing excessive importance to the chosen mathematical function.
I don't understand what is surprising. I would be much more surprised if the majority of the phenomena were extreme phenomena, that is, the opposite of a bell where most of the samples were concentrated at the extreme and a minority in the center or a phenomenon where the number of samples in each value is equal.
R.H.:
The point here is that the article talks about the mathematical curve called the bell curve.
The whole thing is mathematical after all and this is the apparent source of wonder.
I quote: ... well - I regret and do not quote... I went to choose a sentence to quote and I saw that almost every sentence says this and I have a hard time choosing.
Zvi 20, your reference is the opposite of my understanding, perhaps because you are a physicist and I am a biologist and this is precisely the difference between these two fields :). You claim "there are many shapes that look like a bell but do not hold the same equation." However, I see it exactly the other way around - there are many phenomena in nature that are distributed in a bell shape, but the equation you presented does not describe them exactly because it does not assume barriers.
What I want to say here is that the phenomena do not and should not behave according to an equation, but that the artificial equation is supposed to describe the phenomena and predict their behavior.
Okay, I agree with that.
It is important to emphasize that statistical mechanics, at least in the beginning, was completely classical (if I am not mistaken, the Gibbs paradox in calculating the entropy of an ideal gas was the first place where a quantum idea entered) and simply, as you mentioned, it realized that it was difficult and pointless to calculate the trajectory of each and every molecule
deer
I did not try to claim that the bell curve itself has direct implications for statistical mechanics or quantum mechanics, although there are some, at least for statistical physics as you mentioned. The understanding that came initially with statistical physics was that sometimes we don't have the ability to track all the degrees of freedom of a system and we have to treat them statistically, that is, treat the size of the average for the standard deviation or the correlations. The understanding that we do not have access to all degrees of freedom or that these are actually not determined by dramatic laws was based on quantum theory. In my opinion, this concept is fundamentally different from that of classical mechanics in which a complete description of the system is given at any given moment. The bell curve is, in my opinion, the entry of statistics into physics, and therefore I attach importance to it.
R. H.,
The name bell distribution is misleading - there are many shapes that look like a bell but do not fulfill the same equation.
The bell curve we are talking about is a Gaussian shape (e^-x^2 until multiplied by a normalized constant) - such a shape by definition is not blocked between values but extends to infinity on both sides).
sympathetic,
The link you mentioned between the bell curve and statistical mechanics is understood in the Maxwell distribution, or in fluctuations around a thermodynamic equilibrium point. I would be interested in you explaining why you claim that the understanding of the bell curve was so significant for quantum theory - note that in classical statistical mechanics real randomness was not introduced into science - the concept is still completely deterministic and this is in contrast to quantum theory, so in my opinion it is quite different.
Science deals with idealizations. Science compares the phenomena in nature to ideal models that do not exist in practice. For example: a body falling on the face of the earth does not fall.
It has torques and gravitational forces of various bodies, including the moon. Despite all that the simple model of
A body falling on the surface of the earth is a model of a point of mass moving under the effect of the gravitation of the earth without friction. Science also performs the same type of idealization regarding the noise in the experiment and brings it closer to an ideal distribution, i.e. the bell curve. How good the approximation is always depends on the case being examined.
In my opinion, the interesting thing about the bell curve is, first, the technological progress that made it possible in many cases to start talking about accuracy in experiments. When they began to notice inconsistencies between models and experiments and began to quantify this inconsistency, they began to understand the importance of statistics in science. Second, in my opinion, this understanding led to statistical physics and later to quantum theory. The bell curve is the beginning of the introduction of randomness into science!
Yehuda and Mc*El, many phenomena in nature behave in the form of a bell with minimum and maximum values. Who said a bell has to go to infinity?
Take for example the height distribution of humans which starts from a few tens of cm in a baby as a lower limit to let's say 2.5 as an upper limit with close to 7 billion samples that rotate between these values in the shape of a bell.
The intention in my question was not about the mathematics for which it is agreed that there is a bell
Regarding the rest of your answer - there is food for thought here.
Yehuda
Depends on what is included in the term "nature".
I guess if we ask people to randomly pick numbers (positive or negative - whatever they want) - we'll get a pretty good bell distribution.
Of course, even then it will be an approximation because it will be a bell that is "scattered" over a finite number of values while the true bell is continuous, but I suppose that it will still be permissible to refer to it as a bell (since every statistic we will ever compile will be based on a finite number of samples).
Should an experiment like the one I described be called a natural phenomenon? It is already a matter of decision.
In general - the distribution of the same phenomenon can be seen in different ways depending on the measured size.
I can measure a phenomenon that yields only positive values but the same (numerical) results can be represented by the logarithm of the phenomenon and then distributed over the entire actual straight line.
It can, therefore, be - that there are natural phenomena whose distribution is not normal when you look at them in a certain way, while in another way of looking at them it will be normal.
To Michael
You said almost all phenomena in nature do not behave like the bell
I'm trying to find one phenomenon in nature that works like a precise bell and I can't find it
Is it possible that all phenomena in nature do not behave like a bell, and we will always have to use something soon?
Shabbat Shalom
Sabdarmish Yehuda
Almost all phenomena in nature do not and cannot behave according to a precise bell.
Most of them have a minimum that cannot be dropped below (for example, minimums that are related to absolute zero) and the bell curve should, as we know, continue to infinity on each side.
It is all about a convenient approximation, part of its effectiveness comes from the fact that at the limit - the binomial distribution (which is often really easy to explain) - approaches the normal distribution.
You have to read the messages לפני who press submit.
Complex = complex.
Haredi is a modern-day Euler.
Only thing, the idea is a bit old - about 250 years old.
An example of this is of course the formula:
e^(i*pi)+1=0
Look what it is - there is e, pi, a complex number i, and also 0,1, it has addition, multiplication, power and equality!
there is a God!
Ahhh,
Such a reason you seek,
Excellent - you know what it is and I have no intention of getting into fruitless theological conflicts with you
Shabbat Shalom (or for you considering the time - a good week)
Mr. Zvi,
If you have no difficulty why don't you explain the reason.
It is not about proving or calculating integrals
This is "SIB" / "LMH" / "MDU"
Why and why and for what reason normal distributions in physical reality
are expressed in these mathematical expressions.
What is the deep relation to PI and what is the deep relation to e
Don't prove but explain the reason for this connection, can you?
Mr. Haredi,
Of course, there is no difficulty in explaining these two things:
1. The name "bell" is nothing more than a nickname for what is actually the function e^-x^2
2. The area of the bell can be found simply by integration
Fresh, (4)
You must have laughed a refreshing laugh when you wrote.
According to your method, a sea is a collection of puddles and a person is a block of amino acids
The reason for the bell relationship to the exponential function e^-x^2 is more difficult to explain
and the fact that the area of the above bell is PI^0.5
Moshe:
I agree that the central limit theorem should be mentioned in this context, but it does not solve the whole mystery.
For that matter let's look at a very, very large messy pile of rocks. Now we will ask people to build towers by placing stone on stone, each tower from 100 stones taken at random from the pile. The central limit theorem tells us that the distribution of tower heights will approach the normal distribution (and will get closer to this distribution as more towers are built with more stones).
The mystery still remains when examining people's heights for example (what are the building blocks that determine a person's height?) or other types of phenomena that are normally distributed.
Chemistry is physics at a high level.
Chemists are low level physicists.. 🙂
I do not agree that the age of marriage in Belgium and France is not a physical phenomenon, it is a physical phenomenon. Everything in the universe is a physical phenomenon including thoughts that feel like a non-physical thing. It's just physics at a higher level of complexity. Physics, chemistry and biology are all basically physics. Chemistry is physics at a higher level of complexity and biology is an even higher level of physical complexity.
It is worth noting that the fact that the bell curve repeats and appears in many different places is a well-understood phenomenon and is explained by the "Central Limit Law"
http://en.wikipedia.org/wiki/Central_limit_theorem
which every science or engineering university graduate should know.
Ran, by the grace of Dink, will only use his last name.
I don't know who it is, but the name "Adolf" doesn't really have good connotations for me....