In this article I will try to expose the readers both to some of the ways of mathematical thinking and to the beauty of mathematics.

Leaving the box to enter it:
Dedicated to Herman Baer - an inquisitive and lively mind like a teenager in a 94-year-old body
as part of the discussions around Liran Zeidman's series of articles On the great mathematicians, we also got to discuss the question of what is the optimal set of circumstances to "create" a good mathematician.
Since in order to know how to "create" a good mathematician, one must know what a mathematician is, and since not all commenters demonstrated such knowledge, I got the impression that there is room to improve the familiarity of some of the site's readers with the ways of thinking of a mathematician.
Another impression I received is that people's blocking of talented mathematicians is based mainly on admiration for those who are able to perform complex mental tasks and not on admiration for the beauty of mathematics itself.
In this article I will try to expose the readers both to some of the ways of mathematical thinking and to the beauty of mathematics.
I will try to do this by demonstrating a solution to a rather complicated mathematical puzzle - in elementary ways - such that every high school student should understand - and without any reliance on advanced knowledge.
the riddle:
It has been proven that a rectangle that can be tiled using a collection of rectangles each of which has at least one whole dimension (that is, the size of that dimension is a whole number of measurement units), must have at least one whole dimension (in the same measurement unit).
I will prove the claim in three different ways, each of which demonstrates a different facet of mathematics.
I will present the proofs in "chronological" order - that is - in the order in which they occurred to me.
As fate would have it, this order goes from the hardest to the easiest, but since there is no connection between the different solutions, the matter is of no importance.
I recommend, however, to the reader who has given up on understanding one of the solutions, to skip to the next solution which I believe will be easier to understand.
I am quite sure that the last proof will be clear to all readers.
First proof:
This is the first proof I thought of. It may seem a bit cumbersome but its advantage is that it can be easily expanded to any number of dimensions.
The proof is in the negative way.
In this type of proof, it is assumed that the conclusion of the sentence does not hold and it is shown that this assumption leads to a contradiction.
Let's look at a rectangle whose two dimensions are incomplete.
We will fill it with squares whose sides are 1 (and we will also allow ourselves to use some fractions of squares as needed). We will start the filling from the lower left corner.
The result will look like this:
Then, we will start the same process from the upper right corner.
The result will look like this:

All the original squares (black) were divided identically into four parts.
We will treat the entire rectangle as a piece of land and price the different pieces of land according to their location within the original squares as follows (the black square is drawn with a certain magnification so that there is room to write inside it):
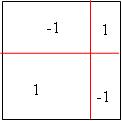
That is, each rectangle within the above-mentioned square will receive the price 1 or -1 when it is sold in its entirety and when a part of it is sold, the value of that part will be determined according to its relative part in the rectangle.
All plots within all black squares will be priced the same way.
It is easy to see that at this pricing, any rectangle that is an integer length or width costs exactly... zero.
The intelligent reader is asked to convince himself of this on his own (the way to see this is to divide the rectangle by lines that are in the direction of the whole dimension, into narrow rectangles bounded between two of the black lines in the same direction in the picture of the large rectangle above).
This means that if the large rectangle can be covered with a collection of one-dimensional rectangles that is complete, then the price of the entire rectangle is zero.
But if we divide the rectangle (two of whose dimensions are incomplete) according to the following division:

It seems that each of the marked rectangles (by a texture unique to each rectangle) has at least one whole dimension and therefore zero is added and from this it follows that the value of the complete rectangle is equal to the value of the unmarked plot which is 1.
It turns out, then, that the assumption that a rectangle whose two dimensions are incomplete can be filled with rectangles that have a complete dimension leads to a contradiction according to which the price of the entire land is equal to zero, on the one hand, and one, on the other hand.
Therefore, we conclude that if the rectangle can be filled with rectangles that have a whole dimension, then it itself must have a whole dimension and this is an error.
The other day someone showed me a proof based on double integrals of sines and cosines that works for exactly the same reason.
The advantage of my way is that it is more elementary (does not require an advanced background in mathematics), more direct (it is clear to everyone why it works) and easier to expand to a high number of dimensions.
Second proof:
This proof is simple and elegant but extending it to some number of dimensions, although possible, is more complicated.
Suppose we have a rectangle filled with smaller rectangles each of which has at least one integer dimension.
In each of the inner rectangles, we will color the sides in the complete direction (if the rectangle has two complete directions, only one of them will be selected for coloring and the completeness of the other will be ignored).
Since the rectangles border each other there will be sections that will be colored twice. We will not ignore this fact - a section painted twice will be recognizable as painted twice.
Let's look at an illustrative example:
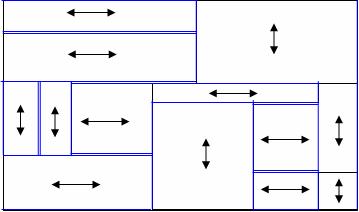
In the example above, the complete direction (the only one that was or the one of the two that was selected) was marked with a two-way arrow.
Sections that have been colored twice appear as a double colored line.
Suppose now that we start walking along the painted lines without repetition (erasing the color from each section we passed through, but if part of the section is painted twice we only delete one of the hypocrisy) when we start our way in the lower left corner of the outer rectangle and move from section to section only where the section is on it Our walk ends and the next section begins (this distinction is important because sections can partially overlap, as you can see in the example).
It is easy to see that every time we finish our trip along one of the sections, we are an entire distance from both the bottom side of the outer rectangle and from its left side (because with each step only one of these distances changes and it changes by an integer number).
At a certain point we will not be able to continue progressing because each time we erase the color from another segment and the number of segments is finite.
If we succeed in showing that this stage will always happen when we are in a corner of the outer rectangle that is different from the starting corner of our path, then we will immediately reach the desired conclusion that, as we remember, at this stage as well, as at every stage along the way, we are at a complete distance from both the lower side and the left side.
To show that the route must end at one of the corners that is not the exit corner, the following facts must be noted:
- We will certainly not return to the exit corner because as soon as we left it we "burned" its only connection with the other points.
- We will never stop at a point where the number of painted sections reaching it is even (because every time we enter we will succeed in exiting and if there are still painted sections that reach the point, their number will still be even because we subtracted exactly 2 - the entrance section and the exit section - from the number of painted sections that reached it first).
– The only points where the number of painted segments reaching is odd (actually exactly 1) are the points in the corners.
The last claim among the three claims above must of course be proven.
We will prove this by analyzing all types of segment end/start points.
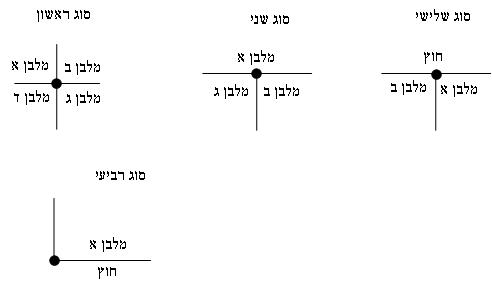
The points of the first type are the intersection of four rectangles. Four painted sections reach the intersection point - one from each rectangle (remember that two painted sections may be in the same physical place).
The points of the second type come with 2 painted segments - one from rectangle B and one from rectangle C. Although a side of rectangle A also passes through this point (and it can also be painted), but this side does not have an end at this point and therefore it is not possible to pass to it or from it at this point.
Points of the third type have two painted segments - one from rectangle A and one from rectangle B.
The points of the fourth type are actually the corners of the outer rectangle and, as mentioned, exactly one painted section reaches them.
parable.
Note that both this method and the previous one are aided by a process known in mathematics as "auxiliary construction".
In the first way, the auxiliary construction is the pricing of the land and in the second way it is the painting of the ribs.
Those who studied auxiliary constructions in geometry in high school can see here that auxiliary construction is a much broader thing that is not even limited to the original world of concepts of the problem.
Anyone who didn't learn about auxiliary constructions in high school probably did in the last few years (as far as I've heard, the high school material no longer includes construction problems in geometry. This in itself is a huge loss in my opinion, but I don't know if students are still "allowed" to learn about auxiliary constructions without being killed for so they know too much).
Third proof:
This, in my opinion, is the simplest and most elegant of all the ways in which I proved the theorem.
Its disadvantage is that it is difficult to expand to a higher number of dimensions, but it makes up for this disadvantage with an additional message that can be illustrated with it, as you will argue.
Let's look at a rectangle filled by rectangles that each have at least one whole dimension.
We will remove all the rectangles from it but we will remember where each one was and we will start putting them back in their place one by one.
By returning them to their place, we will start from the bottom and make sure that each rectangle is returned to its place only after there is something to "place" it "safely" on, meaning that all the rectangles that "carry" it have already been placed.
Below is a drawing for illustration:

In the above drawing, the white rectangles have already been placed and the others have yet to be placed.
The green rectangle can already be put back in its place, but the red one not yet because "its base" is not yet ready in its entirety (before we put the red one, we must put the striped rectangle that is under its right part.
At each step, we will define as "front" the dashed line that describes the highest points that have already been filled.
For example, in the above drawing, after the green rectangle is placed, the front will be described by the thick black line.
Every point on the facade is a certain distance from the base of the outer rectangle.
This distance can be complete or broken (incomplete).
We will characterize the points at the base of the outer rectangle (hereafter "the base") as complete if the facade above them is at a complete distance from them and as broken if the facade is at a broken distance above them.
At the beginning of the process, the front is the base of the outer rectangle and therefore all the points on the base (they are at zero distance from the front and zero is known to be an integer and therefore they are) complete.
Each time an additional rectangle is placed, the characterization of some of the base points may change.
Characterization of a point can only change if we assume a rectangle whose height is incomplete (and then we know that its width is complete).
This means that every time the state of some of the base points changes, it happens to a segment in the base whose length is complete.
Since at the beginning of the process all the points are complete (as mentioned above) and since any change in the characterization of points always occurs on complete segments, we can claim that at each stage the measure of the set of broken points is complete (at the beginning it is zero because all the points are complete and later, when it increases or decreases, it does so only along full-length segments).
So what happens in the end?
At the end, after we have filled the entire outer rectangle, all the base points are at the same distance from the front, so either they are all complete or they are all broken.
If they are complete then we are done because that means the height of the rectangle is complete.
If they are broken, we are also finished because we know that at every step, including this step, the measure of the set of broken points is complete and this means that the measure of the base is complete because the set of broken points is the entire base.
Wow!! No?
It turns out that the problem can be solved simply by….a play on words.
In a previous article I argued that what separates man from the beast, more than it is expressed in the fact that man has a language, it is expressed in his ability to invent language.
This ability helps him to think that he can give a name or symbol to a complex concept and then use this name/symbol in building more complex concepts and thoughts and God forbid.
It seems to me that in this solution you can see how useful this ability is.
Outside our problem world the words "front", "whole" and "broken" are used in a completely different meaning than inside the problem world (who ever heard of a broken point?).
I should point out that I could have chosen other words (such as beeping, smargol and yfarn) for the same need but I preferred to use words that have a connection between their accepted meaning and their meaning within the problem.
Extensions to the original puzzle:
It turns out that the theorem can be extended to a larger number of dimensions.
In its most generalized formulation, the sentence looks like this:
If we have a collection of N-dimensional boxes (not necessarily identical!) each of which has at least K dimensions whose length is an integer, then every N-dimensional box can be filled with at least K dimensions whose length is an integer.
I will not provide a detailed proof of the matter here because the mathematical formalism will make it difficult for the readers.
Instead, I will limit myself to describing the idea of the proof:
First of all, it seems that the first method of proof goes to additional dimensions without any change.
Simply, instead of pricing squares with sides of unit length by dividing them into four rectangles, we will price N-dimensional "cubes" by dividing them into N-dimensional "boxes" (2N such boxes, each of which contains exactly one vertex of the divided cube).
It is difficult to draw it, but you are welcome to try to compare in your mind's eye how it looks in three dimensions. The pricing is done by dividing the outer box into normal cubes, each of which is divided into 8 boxes, each of which costs 1 or -1.
The following drawing (of what should be a 8D cube divided into XNUMX squares) may help:
It is difficult to describe the exact process in a text that is accessible to everyone, but I hope that what I said is still understandable.
For connoisseurs I will add that the price of the box can be determined simply by raising the number minus one to the power of the ones in the representation of the corner of the cube associated with it (where all corners are represented by all possible combinations of N zeros or ones).
Similar to the two-dimensional case, here too it can be seen that a box with one of its entire dimensions will cost zero, and here too we will reach a contradiction in the case where the outer box does not have an entire dimension.
From this we get that when a given collects N-dimensional boxes with a whole dimension, there must be one whole dimension for each N-dimensional box that we assemble using them, but we wanted more. So far we have proved the theorem for all N but only for K=1.
The transition to a larger K is simple.
If there are K integer dimensions for each inner box then surely there is one.
Therefore, the N-dimensional box should have one whole dimension.
Let's now look at the "wig" perpendicular to this dimension - it is actually an N-1 dimensional box covered by boxes
N-1 dimensions each of which has at least K-1 integer dimensions and therefore this box also has an integer dimension and so on.
As I mentioned, a complete and accurate formal writing of a solution to this type of question is extremely cumbersome.
I hope that the present text is sufficient to give those who do not have all the necessary foundation at least the "taste" of the proof and to those who have the necessary foundation all that is necessary to fully understand.
Additional conclusions:
Using boxes whose dimensions are 1x2x4 it is possible to fill only boxes that have a dimension that is divisible by 4, another dimension that is divisible by 2 and a complete third dimension (and all of them).
In general, using boxes with dimensions that are integer multiples of D1,D2,D3....DK If DI divides DI+1 only boxes with the same property can be filled.
Using boxes with dimensions that are integer multiples of D1,D2,D3....DK when the relationships between these dimensions are irrational, only boxes with the same property can be filled.
The mathematically inclined are invited to prove these derivative claims for themselves.
The last conclusion is not true when the relations are rational (because then one dimension of the outer box can "satisfy" several dimensions of the interior).
The energetic reader is invited to convince himself of this by constructing an example.
In issue 112 of Galileo the following question appeared:
Is it possible to fill a box measuring 6x6x6 with boxes measuring 1x2x4?
In response to the question, I wrote that the answer to it is one of the conclusions from a general theorem that can be proven according to which if we have a collection of N dimensional boxes (not necessarily the same!) each of which has at least K dimensions whose length is whole, then every N dimensional box that can be filled with at least K dimensions whose length is whole ( the sentence with which this article was concerned).
I also explained how the answer derives from the sentence but Here I will leave it as an (easy) exercise for the readers.

54 תגובות
Remember the description of the relationship between the ability to invent language and the ability to think effectively?
Here is a nice example from the last few days:
http://www.haaretz.co.il/news/science/1.1827725
"Mochizuki is developing a new language, so it will take a good few years before there is a consensus as to whether it is correct or not,"
For anyone who is interested - there is a claim to prove that P!=NP
Below is a list of relevant links:
http://www.hpl.hp.com/personal/Vinay_Deolalikar/Papers/pnp12pt.pdf
http://rjlipton.wordpress.com/2010/08/08/a-proof-that-p-is-not-equal-to-np/
http://rjlipton.wordpress.com/?p=5206
http://www.geekosystem.com/p-np-proof-vinay-deolalikar/
http://www.hpl.hp.com/personal/Vinay_Deolalikar/
I enjoyed reading.
I know a slightly different wording that allows for a slightly different proof but with exactly the same principles as the second proof.
You dug
Tzviki:
Thank you for your words but there is one thing where you misunderstood my intention.
My intention was to allow those who want to deepen their understanding of the matter - to get a real feeling about it.
There is no way to teach in a pleasant way those who do not want to learn and this article is not intended for such people.
The way to teach such people begins with curbing their convictions and arrogance and that is what I did try to do in the responses.
Dear Michael,
Thank you for your waiting article.
With your permission I will quote part of it:
"It turns out that the problem can be solved simply by….a play on words.
In a previous article, I argued that what separates man from animals, more than it is expressed in the fact that man has a language, it is expressed in his ability to invent a language.
This ability helps him to think that he can give a name or symbol to a complex concept and then use this name/symbol in building more complex concepts and thoughts and God forbid.
It seems to me that in this solution you can see how useful this ability is."
I do agree with you.
At the same time, it should be noted that this advantage is relevant when the people to whom the message is intended do understand these complex concepts and thoughts.
When they don't know each other, and I repeat that I am referring to the target audience you mentioned at the beginning of the article, we will remove the human advantage and the animal remains, which, as we have seen in your responses, also has considerable expressive abilities.
Tzviki
Hi Michael. I created a reference to the riddle and your beautiful article in Gan Adam
thanks Michael . It is interesting. You probably know that this year is called the Year of Astronomy because 400 years have passed since Galileo's first telescope observation at the University of Padua. According to the attached link, 4 problems remain unsolved from the list of Hilbert's 23 problems 6,8,12,16. So the mathematician has more to do..
http://he.wikipedia.org/wiki/23_%D7%94%D7%91%D7%A2%D7%99%D7%95%D7%AA_%D7%A9%D7%9C_%D7%94%D7%99%D7%9C%D7%91%D7%A8%D7%98
Thank you, Moshe.
The truth is that I live all the beautiful problems I have ever encountered and this is only one of many.
I hope to continue living them all for many more years (they say that one who smokes for 120 years lives a very long time).
Herman Baer is the grandfather of the previous editor of the "Galileo" magazine - one of the people who sacrificed the dream of becoming a professional in mathematics on the altar of building the country.
At his extreme age, he still likes to deal with mathematical problems and continues to try to understand the world.
Shlomit Uziel - the previous editor of Galileo thought that the match between us might go well and indeed it was.
Hi Michael
I read with interest your beautiful article "Being a Mathematician" - thank you.
It's beautiful to me that you've been living a mathematical problem for about 40 years!
I especially liked the third proof which I think is the most elegant.
Who is Herman Baer, to whom you dedicated the article?
Moses
Ron:
Unfortunately, what is happening here actually met exactly my expectations.
There are some decent and some dishonest commenters here - just like in any other discussion on the site.
Among those who are not decent - there are those who attacked me personally and your attempt to calm down will not cover up this fact.
Why is it?
Someday - when we talk - I will explain to you how I found out who you are.
The left is not what the right thinks it is and in any case I do not define myself as a leftist of the type you think of.
I have explained on various occasions that I think the "measure against measure" strategy illustrated by the Tit for Tat algorithm in Axelrod's experiment is the correct strategy.
Be decent - never attack for no reason - but when you are attacked for no reason - punish severely.
Well, this post and its comments were blown out of proportion
Michael tried something - and it didn't work as he expected.
Nothing happened, you can try again.
There is a criticism here of the way of presentation, not a personal attack on Paul On and his abilities
Michael, take it easy, there are more problematic attacks...
http://www.youtube.com/watch?v=hiANsBkgqjU
Rafi:
Thank you for your words.
Regarding your question about intuition - see my response 24.
Unfortunately, there is no real answer in it, but that's all I know how to say.
If I were Ramanujan I would say that Goddess Namagiri planted the solution in my mind.
Michael Rothschild:
If you really know who I am, even though I myself don't know who I am, then you really are a first-rate intuitive genius.
And regarding the swelling I still believe that it is possible to praise any existing swelling and allow him to erect a carbolat without insulting.
Apart from that, I wonder what you think is the answer to violence with violence. Because it seemed to Tommy that you were on the left side of the map.
After all, this is usually a hawkish right-wing approach. But it is also possible that the left side has a right side itself.
It's too complicated, maybe you should just adopt a light approach when it doesn't cost anything, life is hard enough.
Michael not Rothschild:
I do not agree with you.
The response to violence should be reciprocal violence.
When this reader apparently came and played the role of Goldstone, I found it appropriate to clarify things for him as clearly as possible.
Why is it?
Since I know who you are - I am surprised at your response.
What swelling of mine are you talking about?
Am I the one who said that the question with the numbers is suitable for elementary without knowing how to solve it myself?
The "student" just attacked me personally without me doing him any harm.
As I said - apart from poison, he contributed nothing to the discussion.
to Michael Rothschild-
Response to response 30
I don't want to get into the matter of who attacked whom, who is trying to show off and who isn't. I want to refer to one sentence that you wrote in your response, and I quote: "There was no trace of arrogance in my response - it was just an attempt to allow this piece of shit to test himself in something that does belong to the topic before he attacks me in areas that do not belong to the topic."
I think that as an official writer on the site, you could have moderated your statements a bit, not descended to the level of the student from the settlement, and not used the word "shit". It is not respectable, and does not add to the level of the site.
Hello Michael,
I would like to thank you for the enormous investment in writing the article. After a very intriguing reading I was able to understand the beauty of each of the proofs.
The choice of steps in each of the solution methods was unique and extremely interesting. Regarding the mathematical intuition, I will agree with Ehud's question.
At this time I am in the stages of preparing for the matriculation exam in mathematics (questionnaire 007), and it is so great for me to see other sides of mathematics that do not usually find expression within the framework of high school studies. I am even seriously considering continuing my math studies at the Technion.
I would love to absorb your love of mathematics in the future as well.
Michael Rothschild:
don't know who i am so how do you know who i am
The things are addressed to all the debaters. to you too
I don't think there is a girl arguing here. For this reason that women are less inclined to inflate their egos in these kinds of things.
In any case, if you are puffing up, then everyone is allowed to puff up. Any cabbage owner is welcome.
Even the tired student needs and deserves encouragement.
You don't have to shrink into pyrgonim.
Why is it?
Before I answer, I would like to know to whom the things are directed.
By the way - I actually know who you are 🙂
Why the aggression? So what if a student wants to puff up in front of Michael. Everyone wants to show that they have more than what kindergarten is. It's just math, not war. And by the way, why should the question of natural numbers scare the student. Suitable for elementary in my opinion.
challenged:
Maybe you didn't understand the proofs but unlike some of the others, at least you understood how to behave so you have nothing to be ashamed of.
I suggest you try to focus on the third proof and overcome the lack of concentration problem you describe.
Try two or three times and if you still don't understand - we'll see what can be done.
I also have no problem meeting you and explaining to you (in a face-to-face conversation I can explain much better the difficulties that are stopping you and help you overcome them).
In fact, this is an open invitation to anyone who is unable to understand the article and wants to receive a personal explanation.
to a student from the settlement
Please allow me to point out that your response (No. 26) is, to say the least, unfair and impolite. First, the author himself in his article insisted on the "language problem" in mathematical problems in general and in the discussed problem, in particular. He explained that words that are used in mathematical problems receive, through their mathematical definition, meanings that are different from their meanings in everyday language. Second, the concepts appearing in the problem were defined in the body of the problem. This is the accepted way in the language of mathematics. You, who identify yourself as if you are a student at the Technion, must have come across this many times
during your studies. Therefore, your argument against what is written in the article is not clear to me.
Finally, a diagnostic note. I would not be surprised to find out that you are an engineering student and not in a scientific subject such as mathematics or physics. I say this because, to the best of my discernment, engineers (and architects) are usually looking for the practical, applied, immediate aspect and the quick technique to get the "right result". Scientists, on the other hand, have a broader view. And they are looking for generalized laws as much as possible for a general description of problems. (both physical and theoretical problems).
Science and mathematics have shown in the past that sometimes it is precisely the generalized approach
(I mean what is known as the inductive approach) may lead to the solution of a wide variety of problems.
I was challenged…
Of course I understood the riddle, what (or maybe not actually?..)
What is certain is that I did not understand the proofs.
On the other hand, I have no mathematical training, that is, I do not know how to read such proofs - my line of thought is too thin, and I forget what the current stage is...
Basically, I don't understand the division into stages, and what is the internal logic (that is, which question should be answered first, in order to establish sufficient knowledge as a foundation for the next question).
Perhaps a paragraph describing the train of thought or intuition underlying each proof would help.
Just reading:
I guess if you see someone who steals someone else's car and he runs after him and shouts - you will scold the one who shouts.
Did you not read the student's excellent and in-depth answer?
What do you think he wanted to achieve in this response?
There's no need for you to bother answering - just read to see that he didn't say anything on the matter.
He didn't pay attention to the riddle or the explanations - nothing - he just decided he wanted to attack me.
I can assure you that in the other cases on which you formed your opinion - the background is similar.
There was no trace of arrogance in my response - it was just an attempt to allow this piece of shit to test himself in something that does belong to the topic before he attacks me in areas that do not belong to the topic.
I attribute your misunderstanding of the matter to the fact that you did not read his words.
To Michael,
Too bad.
I respect your knowledge, but unfortunately some of your answers (in general - and not only this time) hide immodesty. And in your answer to the student (7) even arrogance is revealed.
You can fight - but why fight?
I just want to say that I didn't understand anything from the puzzle or from the reviews
But I'm glad there are people with sense in Israel
A student from the settlement:
What town are you from exactly?
Thank you for your fascinating contribution to the relevant discussion.
Tell me, by the way:
In your town, do you know how to prove that if there is a group of naturals between one and a thousand whose least common multiple of any two of them is greater than a thousand, then the sum of their inverses is less than 1.5?
I hope that your town at least knows that the inverse of a number is one divided by the same number.
be healthy some wording for a puzzle,
I am after a long day of school,
But as a student at the Technion who sees quite a few mathematical proofs on a daily basis,
I had to make an effort to understand the wording of the puzzle, and I only managed that because I read the proofs.
"One whole dimension (ie - the measure of that dimension is a whole number of measurement units)" What are we supposed to understand from this sentence?
What is an integer dimension? What is a measure of a dimension anyway? There are no such concepts.
Missing simple and beautiful proofs with interesting stories? For example, you can show Euler's proof on Eulerian graphs, with the story of the Königsberg bridges (and you can explain it without explaining at all what a graph is).
Michael, thanks again for the beautiful article.
I believe that in order to derive pleasure from a puzzle one must try to solve it. Many of the readers did not try to solve the riddle and therefore it was difficult for them to see the beauty in the solution.
Regarding the missing line when I click on the drawing at the bottom of the image (to get only the image) does it appear as it should? Only when the image is part of the article does the line disappear. Computer gadgets.
sympathetic:
I just noticed that I forgot to answer you about the thing that led me to the intuition of the first solution.
Maybe I forgot because the only answer I can give to this question is "I don't know".
I estimate that it has something to do with the fact that I already noticed before that that sometimes auxiliary constructions really justify the oil and really help.
Building a grid with a complete side on the rectangle seemed to me to be a construction with potential.
The construction of the second lattice may have been carried out for reasons of symmetry.
And then - suddenly I saw the whole proof.
The interesting thing is that everything was in the head - without the use of a string at all.
It is somewhat reminiscent of the story about a very rich man who someone asks him how he made his fortune and he tells the following story:
"I was walking down the street and saw two apples rolling on the floor.
I picked them up, polished them, and bought three apples from the cash register.
I also polished them and sold them and God forbid, so that each time I had more apples...
Then suddenly they called me from some law firm and told me that I was the only relative of some millionaire who passed away..."
A. Ben-Ner and Ehud:
Thank you for your words.
It was clear to me in advance that some people would not understand. I believe that this is not a problem of intelligence, but a problem of willingness to invest, because this is really about things that may be difficult to discover, but in my opinion - anyone who is willing to make an effort can understand.
I base my belief that anyone can understand the things on serious experience I acquired many years ago in giving private lessons.
Students came to me with an average of 4-5 grades and usually after a limited number of lessons they reached an average of 9-10 when the main effort I invested in them was directed to restoring their self-confidence and renewing their love for the subject.
Yes! Novelty! It is much easier to find a toddler who loves math than a high school graduate who loves math and the reasons for this are many.
You can blame the teachers and certainly they bear part of the blame, but the problem is more of an environment that has two destructive elements:
The one element is that people take pride (yes! Unbelievably, but they do!) in their inability to deal with math problems (of course this is just an external behavior but it is a contagious behavior that is easily adopted by any student who encounters any problem).
The second component is a curriculum that does not emphasize the beauty of things and the great pleasure that can be derived from a deep understanding of things. It's very sad when you compare it to people's attitude towards art. For some reason people feel comfortable appreciating art even if they are not artists, but in the study of mathematics there is such a competitive atmosphere that fuels the phenomenon I described as "the first element" and in addition creates a situation where people who are not mathematicians by birth also cannot appreciate the beauty in things.
The damage of competitiveness became clear to me at a very young age.
My father's job required our family to move our place of residence from country to country many times.
In fact - with the exception of the first 4 years of elementary school, I did not spend more than two years at the same school.
It's a devastating thing that greatly affected my brother's studies, but I always fell on my feet.
In the last school I was in (Belgian school in Germany) there was a student with whom I very quickly found a common language because he also liked math and puzzles.
The problem was that it didn't take long for him to find out that I surpassed him in my abilities and the result was - amazing as it may sound - that he stopped loving math.
It was an important lesson for me, but not one that I learned immediately, but one that I understood only after several years and I tried to apply this lesson in private teaching.
People need to be made to be able to see the beauty without it evoking feelings of inferiority in them (which in the end find expression in a display of distaste for mathematics or in sarcasm).
I still recommend to anyone who didn't try hard enough to understand - to make an extra effort.
Trust me it's worth it!
sympathetic:
Regarding your comment on the diagram - I do not see the phenomenon you are talking about.
In fact, the three diagrams of the rectangle in the first proof were created from each other (I created the rectangle with the black lattice, then I placed the red lattice on the same rectangle, and then I placed on the result the texture that you see in the third) so it makes sense that a line that is missing in the first will also be missing in the second, but in that case it should to be missing on Tuesday too.
In any case - I don't see the lack you're talking about and I also don't see squares in the column of rectangles (the column of rectangles is intentional because the length of the side is not complete and therefore the rectangle is not divided into squares).
It seems to me like some problem with the display of your browser but the truth is that even if I wanted to cause such a problem I would not know how to do it so for me it is currently a mystery.
If I'm not mistaken, then in the illustration to explain the first proof, there is no black line, the large rectangle is divided into squares, and then suddenly a column of rectangles appears that actually contain a pair of squares. The missing black line also does not appear
In the second figure.
Michael
I take off my hat. Absolutely beautiful proofs.
Although it is difficult to articulate a mathematical intuition, what made you think of the first proof? It seems that the "natural" way to arrive at this proof originates from two-dimensional integration, but you mentioned that you only heard about the proof through the double integral later.
For those people who were looking for a frame story for a puzzle, you can think of a laser resonator. so that a certain box
There will be a required resonator because it will have a dimension equal to a whole number of half wavelengths. So you can ask
Is it possible to assemble a box or a rectangle from a collection of rectangular resonators so that no resonator is created?
In my opinion, the choice of a riddle was an excellent idea because the beauty of mathematics can be presented simply geometrically. Because such a demonstration hardly requires any prior knowledge or concepts to be explained.
To all those who comment like: "I'm a person from the settlement, so I don't understand what's written"
or "the article is difficult to understand...blah..blah..blah" Well gentlemen,
A thousand - you don't have to read every article that is published.
Home - it's not a disaster to read an article two or three times... make an effort... at the end of it
can pay off.
All this provided that your time allows you to do so.
And Michael - thank you, it's interesting to remember my university studies ~30 years ago.
Michael,
You tried to explain. So you tried. And although I appreciate it (!) it turned out that you went to find a kingdom - and you found Athens...
The beauty of mathematics will not be found by the lay reader, and by the way - he will even feel like an idiot.
It seems that the beauty in which only the open-eyed can see, and those who do not have those very specific inter-neural connections in their brain will continue to admire the mathematicians - but they will continue to be strange birds to him in one way or another.
Did the explainer fail - or maybe the math flew higher and higher?
both.
And I'm down here with the crowd...
Ron:
I'm not investing in you.
Eran:
By "exposing impostors" I did not mean anyone who responds here but to all kinds of people who in all kinds of discussions try to teach me to think and even teach me math (and pretend to be those who understand the matter).
Simon Singh may be known as a wizard but he doesn't deal with mathematical problems.
Maximum it shows their results.
That's not what I was trying to do here.
I have no problem with the review.
To Michael:
I'm interested to know why you intend to expose imposters?
A few small things:
1. First thing, strive for the hard work, see the investment.
2. What I meant to say is that very few people can relate to the article, for the simple reason that writing an article of this type that will be both interesting to people who studied (at least) the basic subjects in the field at university and also be clear to laymen is a very complicated thing and few are capable of it. It is not for nothing that Simon Singh is considered to work magic in the field.
3. I will try to read the article again, this time to the end.
4. Strengthening criticism, isn't it?
As I said - solutions to this question (which I solved about forty years ago (really!)) have already been published and today you can find some of them on the Internet.
For example here:
http://www.inference.phy.cam.ac.uk/mackay/rectangles/
Here:
http://www.helsinki.fi/filosofia/filo/jvp/coquand.pdf
Here:
http://sbjoshi.wordpress.com/2008/07/31/rectangle-tiling-problem/
Here:
http://mathdl.maa.org/images/upload_library/22/Ford/Wagon601-617.pdf
and in many other places.
It seems to me, however, that despite all the years that have passed, the third proof I described is still unique - both in its simplicity and in the thought tool it uses.
Michael
You are in the role of the teacher, I am in the role of the student
I wanted to understand
I'm a person from the settlement and I didn't understand anything, certainly not the riddle.
Maybe a riddle related to something practical (maybe even a story) that I can imagine is better
with gratitude
Friends:
Since a point suggested an article about the infinity of the set of prime numbers, I decided to simply add a comment here proving it.
The proof is a simple proof by way of negation.
Suppose there is a finite set of primes that we will call P1,P2,P3,……Pn
If we look at the number P1xP2xP3x....xPn +1 then this number is not divisible by any of these primes (because there is always a remainder of 1 in the division) and therefore it must either be another prime itself or be divisible by another prime that does not appear among the aforementioned primes.
In other words - we have shown that every finite set of primes has at least one prime that is not in it, and that is a prime number.
Jones:
The article has already been published.
I tried to formulate the question more simply in the comments.
I assume that in the end you understood the question because otherwise you couldn't understand the proofs (because you couldn't understand what they were trying to prove).
I don't know exactly what the point of a point you agree with and above all I would like to know if there is anything you are asking of me in this regard.
As a matter of principle - I knew in advance that this was a somewhat heavy article for the science site (and my father and Roy also warned me about this point in advance), but I thought there was a point in publishing it now precisely because the comments I read in various articles (mainly those by Liran Zeidman) showed me that something of this kind is necessary for certain people (Probably - not those who responded here - none of whom responded to the wording of the question that I posted even before the publication of the article).
I understood the evidence but not the question
I agree point by point
Another thing for Eran M:
I certainly could have written an article on a different topic and it would certainly have been simpler and there might have been more readers.
Moreover - I also wrote other articles.
The point is that the content of this article cannot be conveyed in a completely simple way, nor can the feeling of what it is like to solve a mathematical puzzle.
In the discussions here I presented here and there solutions to simpler mathematical puzzles.
I also presented some puzzles that are no longer simple, but I did not present their solution because unlike this puzzle - their solutions were not published anywhere and this allows me to use them to expose imposters.
I don't know how you define a person who is "accessible to math" but a lot of people who are really "accessible to math" have read different versions of this article and I have to say that the responses from those people have been really enthusiastic.
The thing is, of course, it's not for those who are lazy to think.
Boris:
I mentioned this proof in the article but it is not simpler but much, much more complex.
Among other things, she needs to know how to do double integrals and even then it's not completely trivial.
Eran M:
You say this even though there is no formula in the article?
point:
I didn't want to bring anything trivial.
I might have had to settle for the third proof which it seems to me that none of you have reached despite my warnings.
There is a saying that every additional equation cuts the amount of potential readers in half.
As someone who is actually accessible to mathematics I could not read it.
There is a much more elegant proof:
Take a double integral over
sin(2*pi*x)*sin(2*pi*y)dx*dy
on the area of the entire rectangle.
It is quite easy to prove that the integral zeros if and only if at least one of the sides of the rectangle is complete (exercise!).
Since an integral over a rectangle is equal to the sum of the integrals over its division and every integral in the sum zeros, the integral over the entire area zeros. Hence the rectangle has a complete side. parable
Of course, the proof can be extended to any dimension.
The first thought that came to my mind is "what is this vague wording of the riddle"
A second thought says that maybe a mathematician reading this sees a simple sentence like x+x=2x
Agree with dot's point.
It is difficult for a person from the settlement to follow the article.
My opinion is that the puzzle is too technical and does not show what you were trying to show... and it would definitely be better to use length/width. And also adds an example that illustrates what the riddle is asking.
Perhaps it would have been better to come up with something cleaner and more elegant, something like the proof that there are infinitely many prime numbers. which involves only one dimension.
Maybe it can be phrased like this:
Given a rectangle that is tiled by inner rectangles (not necessarily equal).
Given that in each of the inner rectangles - the length or width is a whole number of centimeters.
It was proven that even in the outer rectangle - the length or width is a whole number of centimeters.
There is a bit of a problem with this wording because someone may not understand that this is also true for millimeters or inches and perhaps he may also not understand that there is a possibility that both the length and the width will have a whole measure but it may be possible to waive these matters.
incidentally:
One of the reasons I posted the riddle first (in the Ramanujan article) was to make sure people understood it.
There were questions and clarifications and the current version tries to answer the difficulties that arose there.
In principle, I would like to use the terms "length" and "width" instead of "dimensions" but there is a problem with phrases like "the length of the length" or "the length of the width"
point:
Did you finally understand what the riddle was?
Do you have a suggestion for alternative wording?
Michael Shalom, thank you for the articles you write, and for the effort you invest in instilling the love of science and the right thinking to all readers who want to know for the sake of knowledge.
I would like to point out that at the beginning I did not feel comfortable with the wording of the first riddle, it may be worded precisely, but it is certainly not worded in a clear way for a person from the settlement who is trying to understand what the riddle is asking, and this is exactly the kind of thing that I think keeps people away from science in general and mathematics in particular. And that's exactly what the article is about 🙂
Correct me if I'm wrong.