What is the correct strategy when choosing between two identical sealed envelopes, one of which contains twice the amount of money as the other, if we are allowed to change our minds after the first choice?
Marius Cohen, "Galileo" magazine
The paradox: we are presented with two identically shaped envelopes, both closed and sealed, so that it is impossible to see their contents, and we must choose one of them. We are told that each envelope has a certain amount of money, and the amount in one of the envelopes (we are not told which one) is double the amount in the other envelope (let's also assume that the money is in the form of a check, so the envelopes are also the same in weight and volume).
Since it is impossible to know how much money is in each of the envelopes, our choice of one of them is random. However, immediately after choosing one of the envelopes, we are offered the option to exchange between them, that is, to return the envelope we chose and receive the other envelope in its place, which, of course, has either double the amount of money that we currently have, or only half of this amount. Should we make the switch or stay with our initial choice?
Apparently it seems that in terms of the chance of winning the most money it doesn't matter if we stay with our initial choice or switch envelopes, since there is no external difference between them. Likewise, we could have just as well chosen the other envelope first, and had the option of replacing it with the one we actually chose.
On the other hand, suppose the amount of money in the first envelope we chose is A shekels. The amount of money in the other envelope is therefore either 2A shekels, or A/2 shekels, so that the exchange between the envelopes will result in either a profit of A shekels or a loss of A/2 shekels, and it seems, therefore, that exchanging the envelopes would actually be a good strategy (if we can To give up 100 shekels and in return receive either 50 shekels or 200 shekels, it seems that the risk of a small loss justifies the chance of a large profit).
For those who are familiar with the concept of expectancy, here is a suggestion for calculating the feasibility of the exchange: since the amount in the other envelope is either 2A or A/2 with equal probability (on the face of it, there seems to be no reason to assume a higher chance for one of the two options), then the expectancy of the amount we will have after the exchange is:
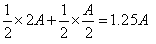And this is compared to A shekels that we currently have at our disposal. The meaning of the life expectancy calculation is that if we are offered to repeat the game a large number of times, and each time we choose the replacement strategy, in the end we will accumulate 25% more money than if we choose the non-replacement strategy (if we give up 100 shekels 10 times, and in their place we receive, let's say , 5 times 50 shekels and 5 times 200 shekels, after all, for the 1,000 shekels we gave up we will receive 1,250 shekels).
To refine this thought experiment a bit, let's say that the amount in one envelope is 100 times greater than the amount in the other envelope. In such a case, it seems that changing the envelopes puts the chance of earning 99A shekels at a clear advantage over the chance of losing 0.99A shekels (if A is, say, 1, then we risk losing 99 shekels from the shekel we have in exchange for the chance of earning 99 shekels).
But again, the envelopes are completely identical, and we could have chosen the other envelope the first time as well, and if it is worth replacing envelope A with envelope B, it is unlikely that envelope B should also be replaced with envelope A. Also, if we are again offered the possibility to switch between the envelopes (after we have already switched between them once), then according to the considerations of the switching strategy this will again be worthwhile. But changing the envelopes twice is equivalent to not changing them at all! So is it worth switching between the envelopes or is there no advantage in such a switch?
This paradox was presented in 1989 by Barry Nalebuff, an expert in game theory from the Yale University School of Management, who based the paradox on a similar idea by the Belgian mathematician Maurice Kraitchik from 1953.
points for thinking
One of the assumptions that led to the acceptance of the exchange strategy was that, after we have already chosen one of the envelopes, the probability that the amount of money in the other envelope will be double that in the envelope we chose is equal to the probability that the amount of money in this envelope will be only half of it. Is it really so? Assume that the amounts in the two envelopes are NIS 100 and NIS 200. If you chose the envelope with the 100 shekels (without knowing it), then the other envelope has double that amount; However, if you chose the envelope with the 200 shekels, then the other envelope contains only half of this amount, but it is not the same amount in both cases: if the amount in the other envelope is double, then it is double the 100 shekels, but if the amount in it is only half, After all, this is half of 200 shekels!
The main assumption that led to the rejection of the replacement strategy was that the two envelopes are exactly the same, therefore a replacement between the envelopes is actually equivalent to a different initial choice, and it seems that there should be no difference in terms of the chances of winning if one chooses one envelope or the other. Also, suppose the two envelopes are delivered to two different people. If the exchange strategy is the right one, then both people will be interested in exchanging the envelopes, but it is impossible for such an exchange to be worthwhile for both! Considerations of this kind are called symmetry considerations, and they have a great deal of persuasive power. Is the symmetry between the two envelopes a sufficient reason to reject the replacement strategy?
Solving the paradox
The exchange strategy was justified above on the basis of this consideration: if the amount of money in the first envelope we chose is A shekels, then the amount of money in the other envelope is either 2A shekels or A/2 shekels, so an exchange between the envelopes will with the same probability result in either a gain of A shekels or a loss of A / 2 shekels.
But this is a misleading representation of the state of affairs. In fact, we are presented with two envelopes, one of which contains A shekels and the other - 2A shekels. If we randomly chose an envelope that contains A shekels, and we choose to exchange it with the other envelope, we will earn A shekels, but if we chose an envelope that has 2A shekels, then the exchange between the envelopes will end in a loss of A shekels! (Or, if the amounts in the envelopes are A NIS and 100A NIS, then our chance of earning 99A NIS is against our chance of losing 99A NIS as well).
Hence the amount we might gain is equal to the amount we might lose, so it doesn't matter if we stay with our original choice or switch between the envelopes. The previous way of presenting the possible profit versus loss was correct if we were given an envelope with money (say NIS 100), and only after that was placed in another envelope with the same probability either an amount of money double that or only half of the amount, and then we were offered to make the exchange. So, if we had switched between the envelopes, we could have received NIS 100 or NIS 200 instead of the 50 shekels with equal probability, and the possible profit would have been greater than the possible loss, which would have justified the exchange. But as we have seen, these are not the rules of the game.
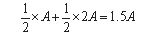In terms of longevity considerations, if we stay with the original choice, the longevity of the amount we have is calculated based on the fact that the chance that the envelope we chose has A shekels is equal to the chance that it has 2A shekels:
If we switch between the envelopes, the new span will actually be equal to the old one:
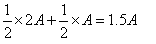(only the order of the connected ones changed), which again proves that it doesn't matter if we stay with our initial choice or switch between the envelopes (as expected from symmetry considerations). On the other hand, the calculation of the expectancy presented at the beginning corresponds to the second scenario, where the amount of money was put into the other envelope only after we chose one of the envelopes, with a probability equal to double or half of the amount in the first envelope.
Dessert
Suppose you were offered to participate in a game of this kind, and before you were offered the exchange option, you were allowed to take a look at the amount placed in the envelope you chose (but you were not allowed to take a look at the other envelope, where the amount of money is either double or half of what you have). Were your considerations different then? Suppose you have come to the conclusion that under such conditions the exchange is indeed worthwhile. But then even when you were not allowed to open the envelope, you could use the knowledge that you opened it and you would choose to switch between the envelopes, and on the basis of this information choose the replacement strategy (which, as we saw above, is not justified).
Also, how might the psychological dimension, which is not relevant to the original problem, affect your decision in the new game conditions? Would you be willing to risk 999 shekels out of 1000 for the chance to become a millionaire? (if, for example, you found a check in an envelope for a total of NIS 1000, and you were told that one of the envelopes contained 1000 times more money than the other envelope), or would you be willing to risk the chance of your life to become a millionaire (if the check you found is for a million shekels) for the chance to become billionaires?
Originally published in "Galileo" magazine
17 תגובות
In my response to the article "To infinity and beyond" I gave the exact definition of a paradox - a logical argument that turns into something illogical because of the huge errors in the way people think. I'm not saying that we are all mentally disabled here, but no one is perfect. Think for a second: what will happen in the universe if a logical contradiction is found that has no solution? It just won't happen. And what if it does happen? As you understand, this boring conversation can go on and on. So let's just leave it at that.
I can actually easily refute this paradox, with the help of some facts and definitions (you will surely understand how it refutes the paradox..)
A. Expectancy is something that only works on a very large number of experiments, games, etc., the bigger the number, the closer it is to expectancy.
B. If there are 2 things that are identical to each other from our point of view, then from our point of view it is possible to derive the same amount of profit (or loss) from both.
third. It is forbidden (in mathematics, it is not that you will be punished for it, I hope) to mix in only one calculation (a sort of "chain exercise") an expectation and a normal average.
And by the way - the solution I most identify with: you simply do half an E multiplied by 2 E in the root, and of course it comes out E (why? Question for thought).
It's a good site but don't need much it's a good site for our knowledge
scholar:
You're right.
I know these things and unfortunately the author did not address the solution of the paradox at all.
As I have said on other occasions - the solution to a paradox is to point out the error in consideration that leads to the wrong conclusion and not by presenting another solution that leads to a correct solution.
Here, as you mentioned, the problem is actually the assumption that there is a distribution function that gives an equal chance to every number on the number line, while everyone who understands the matter knows that such a distribution function cannot exist because the integral of every distribution function is one.
I know, of course also what the strategy is but since you wanted people to think about it I won't go into detail at this point. I am unsure, in light of the responses that have come up so far, if anyone even understands what we are talking about (this is why I have refrained from commenting until now even though I have seen the article before and noticed the errors in it)
The problem is known and a version of it was published with its solution in Scientific American in 1985 if I'm not mistaken.
The paradox is much deeper than the question of profit versus loss, and basically deals with the question "does there exist a uniform probability distribution over an infinite range and it is clear that there is no such distribution".
As for the actual solution, assuming you see the amount in the first envelope, there is a strategy that gives you more than 50% chance that after deciding whether to switch you will stay with the envelope with the larger amount.
The above is true if one of the envelopes has double the amount of the first, and also when there are just two envelopes with one containing a larger amount.
It is even more surprising to find that even if the exchange strategy is advertised, and the amounts in the two envelopes are chosen in such a way as to reduce the effectiveness of the strategy as much as possible, still in the long run the strategy of the recipient of the envelopes is more than 50% effective.
Hint for those interested - this is a probabilistic strategy.
The question is - how will you feel afterwards?
The first choice is luck
The second choice is greed
da
very simple ! Why complicate things?
50% in this direction therefore:
A*0.5 + B*0.5= total profit!
That is, let's assume that A=1 and B=999 therefore:
Profit = 0.5+499.5 = 500
And so on in the other direction.
In general, the average profit = (A+B) /2
Probability, chance and risk, the starting point, and destiny:
According to the figure: we are told that each envelope contains a certain amount of money, and the amount in one of the envelopes (we are not told which one), is double the amount in the other envelope; one of the interpretations of this figure, which say with certainty the amounts; If this interpretation is correct, then if it is a large amount, so that even half of it, will constitute adequate compensation, it certainly does not matter; Even with small amounts, the consideration of whether to make another choice is not significant; And in the event that it is a section of sums between the maximum and the minimum; Sometimes good luck plays into a person's hands, and he wins.
Amazing!! I started driving people in the office crazy with the puzzle, and now everyone has a headache!! Thanks!
Your point of view is not "correct".
From the definition of the problem there are only 2 options.
*
The higher amount in envelope A, or the higher amount in envelope B.
*
The paradox can be seen in the following way.
Suppose there are two games:
In game A there are two envelopes of 50 and 100
In game B there are two envelopes of 100 and 200.
The choice between the two games is completely random (for example by tossing a coin) the participant does not know the type of game chosen and must choose one of the envelopes.
If the participant knows the amount in the envelope he chose, then there is an optimal replacement strategy (to replace if there are 50 or 100 and not to replace in the case of 200).
The interesting case is when the participant does not know the amount in the envelope he chose. The only thing the participant knows is (like the original example) that there is a 50% chance that the second envelope contains double the amount and an equal chance of half the amount. Is there an optimal replacement strategy in this case?
First we will analyze the probability that the participant will choose each of the amounts.
50 - the probability of choosing game A (which is 50%) is double and the chance that he will choose an envelope with 50 (also 50%) therefore 25%
100 - 100 appears in both games so the chance is 50%
200 - calculation similar to the case of 50, i.e. 25%
Now we will analyze the profitability of the replacement strategy in each case:
50 - receives for sure 100 therefore a profit of 50
100 - an equal chance that the second envelope is 200 (a profit of 100) or 50 (a profit of -50) therefore the average profit is 25
200 - definitely lose 100
Now we are left to calculate the average profit which is the product of the odds by the profits
25%*50 + 50%*25 + 25%* -100 = 0
Certainly not knowing the amount increases the number of options.
As soon as you don't know what the amount is and which of the envelopes is the largest (exactly as explained in the article) you have exactly 3 amounts
XX/2 and 2X
But as said
Only 2 options can be realized
The trick here is in the data
Since you don't know which of the envelopes is bigger
, you don't know what the amount is and you choose an envelope with amount X
So you don't know if the second contains X/2 or 2X
Therefore there are 2 options here for the given variable X which is the amount in the envelope you selected
The "redundant" option is only relevant to the statistical calculation of "is it better to replace"
I will refine the example with real numbers
Placed in front of you are 2 identical envelopes blah blah blah as it says in the article
You have selected an envelope
There are 100 shekels in it - but you don't know that
A second can be either NIS 50 (X/2) or NIS 200 (2X)
After all, you don't know the amounts involved and you don't know whether you chose the envelope with the larger amount or not
And from here the statistical calculation of the article continues
The second time you make the selection
You may know that the relevant amounts are 100 and 200 NIS and not 100 and 50 NIS
But you don't know what you chose
at 100? at 200?
If you chose 100 then you have either X or 2X
If you chose 200 then you have either X or X/2
Therefore, the three options enter the equation
Don't forget that we are dealing with statistics
These are theoretical possibilities - not what actually happens
Indeed, a mistake. Need 3 possibilities. And the chance increases. which is 2 really no change.
Miko, here is your mistake.
The fact that you don't know the amount does not increase the number of its possibilities.
Here's your mistake
You don't know what the amount is, so there can be exactly 3 values here
XX/2 and 2X
hearing
Assuming X = 100 and you chose the larger envelope between the two, then the second envelope contains X/2 and therefore 50
and assuming X=100 and you chose the smaller envelope between the two, then the second envelope contains 2X, therefore 200
Your claim is correct if you know the amount and you know which of the envelopes you choose
Already in the presentation of the paradox, and without delving into it, one sees that the paradox stems from an incorrect presentation of the problem.
In the initial analysis of the paradox, it is about three amounts - 50, 100 and 200, while in practice there are only two amounts.
Let you take it