alongside climate researchers, The Nobel Prize in Physics was awarded this year to Giorgio Frisi for his scientific contribution to the understanding of complex systems. The prize committee decided to focus on the solution he proposed to the spin-glass problem on the grounds that this model is able to explain many phenomena outside the physics of materials. What is a spin-glass phase and what is Frizi's contribution to the theory?
More on the subject on the science website
- "Nobel winners Manaba and Hasselman have brought enormous benefit to humanity by providing a solid physical basis for our understanding of climate" (Frisi's Partners for the Prize)
- The climate crisis reaches the Nobel Prize in Physics: two of the developers of the climate models and a researcher of complexity won the Nobel 2021
- Nobel followed Wolff again in the same year: and this time Prof. Giorgio Frisi

Dirt is often a nuisance. The lazy people we built sweep it under the table or under the carpet, but sooner or later it cannot be ignored. In physics, "impurity" is synonymous with a defect in a crystal or disorder in a periodic pattern. If the skeletal structure is slightly destroyed, the infection is not noticeable at all. On the other hand, if the contamination is significant, the interaction between the residual particles is complex and branched. This is because symmetrical patterns simplify calculations and disorder increases complexity.
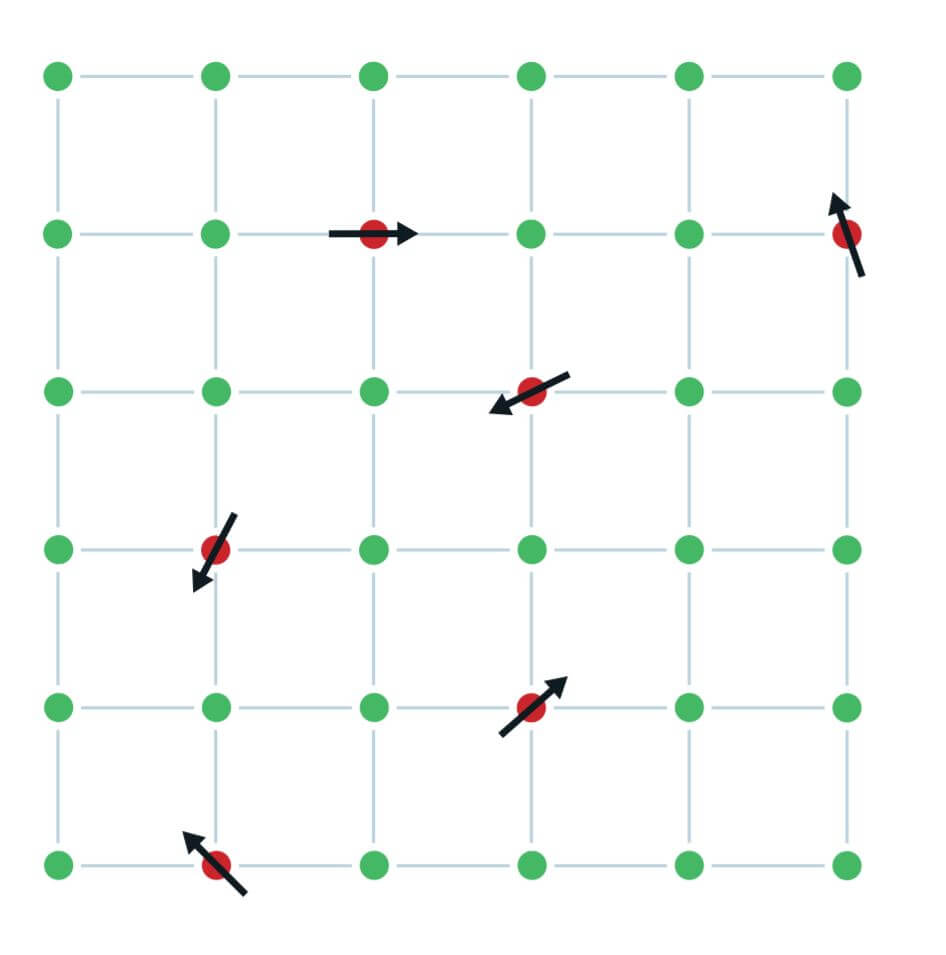
Throughout history, the dirt has been swept away from the lab table or scientific papers to focus mostly on simple systems like pure periodic crystals. In the XNUMXs the trend changed - physicists began to add defects to the crystal on purpose to understand the structure of the glass. The atomic structure of glass is complex and fascinating. The atoms that make up the glass appear frozen in place, just like a solid, but not arranged like a crystal. The lack of symmetry in glass makes it difficult for theorists to mathematically describe how glass is formed, so physicists relied mainly on scientific experiments. The initial experiments that mixed defects into the crystal failed because the amount of defects was so small, similar to the differences in dirt between a newly formed plate and a plate that had been thoroughly cleaned after being immersed in a mud bath. The experimental breakthrough came from a slightly different direction thanks to materials with a phase known as "spin-glass". The first lattice created in the laboratory and found in such a state of aggregation was composed of iron atoms scattered within a copper lattice. The name spin-glass consists of the welding of two names: spin, indicating the fact that the iron atoms have internal spin, or in other words have a small magnet with a defined directionality, and the word glass indicating the fact that the spins are randomly oriented in different directions and that the strength of the forces acting between the spins is completely random. The lack of order in the directionality and strength of the interaction between the spins of the iron atoms is the "dirt" that creates a new and stable structure of the material (or in other words, an exotic state of aggregation).
Spin-glass and magnetic materials
To understand how different the "spin-glass" phase is from other magnetic materials, we will conduct a brief review on "classical" magnets in nature. Materials made of atoms with spin are cataloged according to their response to changes in temperature and magnetic fields. For example, at low temperatures, iron is a ferromagnetic material because it "remembers" the magnetic field applied to it, meaning that the spins tend to line up with the direction of the magnetic field and are frozen in that direction even after the field is turned off. At geological sites, ferromagnetic metals (iron, cobalt or nickel) help researchers measure the Earth's field throughout history. The ferromagnetic property is essentially quantum and the reason iron is a ferromagnet is due to the fact that the energy cost to align in the same direction is smaller than the opposite direction. At high temperatures, above 771 degrees Celsius, the spins in iron will tend to arrange themselves randomly without an external magnetic field. In this state, the iron is in the paramagnetic phase, meaning the spins "do not remember" the magnetic field when it is off. Below the critical temperature, the connection between the spins is stronger than the thermal energy and the metal passes into the ferromagnetic phase in which the spins tend to line up in a uniform direction (depending on the external field or in a random direction without an external field. In this situation the metal becomes a magnet. Most of the time the spins line up in domains, in other words the metal is divided into oriented regions uniform magnetic). Compared to iron, a lattice made of chromium atoms behaves in the opposite way below its critical temperature. Instead of the internal magnets aligning in a uniform direction, each atom directs its internal magnet opposite to its neighbors. This phase is called antiferromanganese, and at low temperatures the chromium does not create a magnetic field.
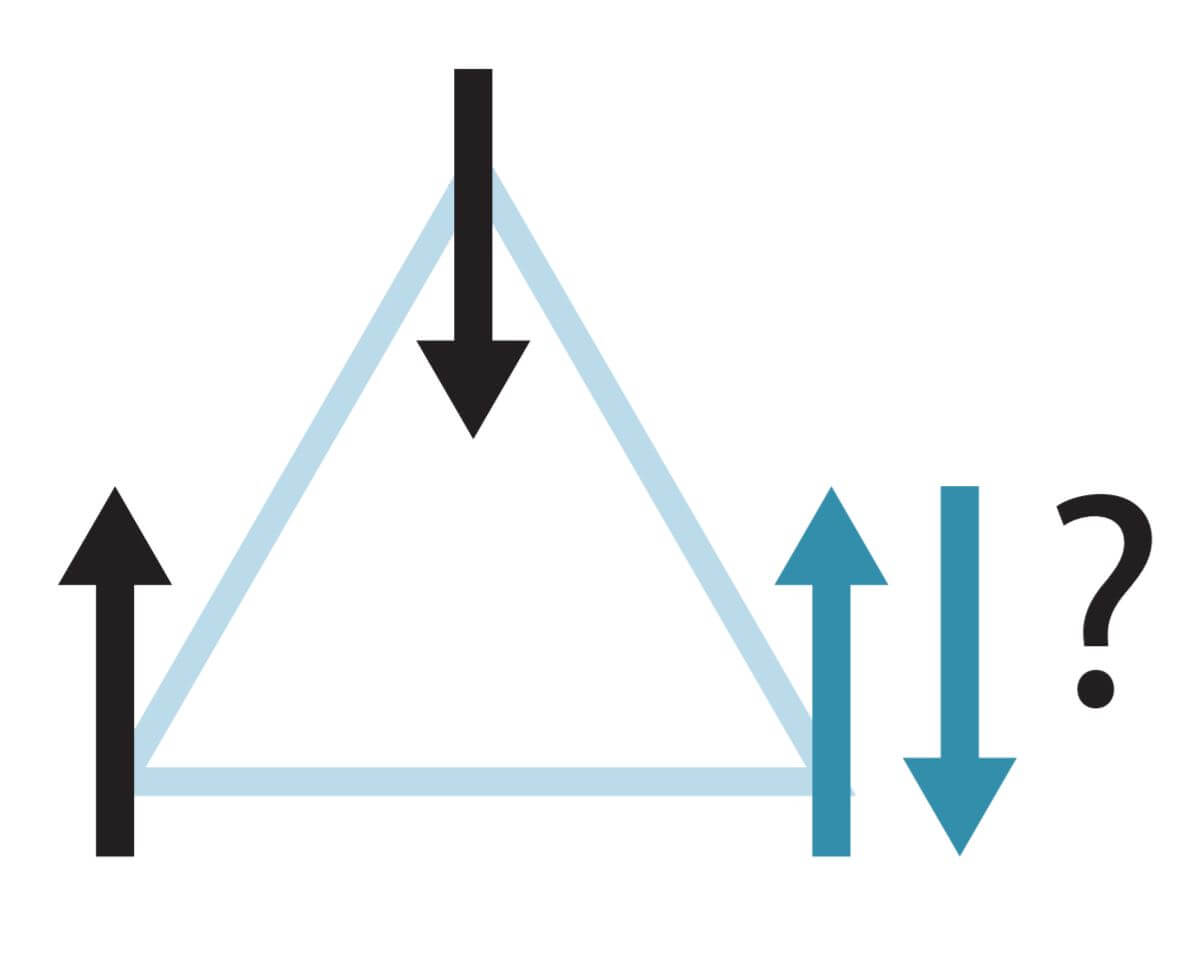
The spin-glass phase is a sort of combination of the two. Spin-glass is created from a non-magnetic outlier with spin-less atoms and magnetic atoms scattered within it, i.e. with a non-zero spin. The bond between the magnetic atoms can be ferromagnetic or antiferromagnetic, meaning that the neighboring atoms will tilt the internal compass in the same direction, or in the opposite direction from each other. Although at low temperatures the iron is ferromagnetic in nature, when dispersed in copper wire it can also behave as an antiferromagnet. The reason for this is due to the free electrons moving on the lattice. Electrons have half spin and their direction is affected by the spin of the iron atoms. This complex reaction creates an effect that allows neighboring spins to align in the same or opposite directions. The strange effect sometimes creates insoluble patterns. Let's say, for example, three iron atoms randomly scattered in a lattice. Three atoms form at most three bonds (atom1-atom3, atom2-atom3, atom1-atom2). The bond to remind you can be ferromagnetic or antiferromagnetic randomly. Suppose one of the bonds is antiferromagnetic and the remaining two are ferromagnetic. You can convince yourself that it is not possible to choose a definite directionality for each of the atoms that will provide the nature of the bond between them. This state is called by physicists a "frustrated" state and sometimes it is said that the spins themselves are "frustrated". It turns out that the steady state of the system is the state with the least frustration.
Frisee's discovery
The frustration problem has led researchers to ask whether spin glass is a new phase in its own right or is simply a very slow paramagnet. The transition between ferromagnet and paramagnet in metal is sharp and clear as the sun. On the other hand, in spin-glass and at low temperatures there is a small magnetic field that gradually fades. At the same time, glass is basically considered a liquid, but its flow rate is very slow. This point of view led researchers to assume that the spin-glass is a very slow paramagnet, but to notice the disappearance of the magnetic field you would probably have to wait longer than the age of the universe.
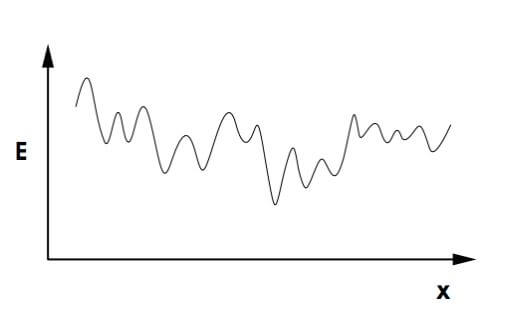
In the 1975s and XNUMXs, several mathematical models were developed to describe spin-glass. To simplify the problem, in XNUMX Sam Edwards of Cambridge University and Philip Anderson of Princeton University tried to describe a system in which the spins respond only to the nearest neighbors. The assumption turns out not to significantly ease the calculations and Sam and Philip's model is found to be incredibly complicated with a huge number of states with local minimum energy (the preferred state for physical systems). Locality means that energy is required to make minor changes in the system, but at the same time if we invest enough energy we can be dragged to a lower energy state. After that, David Sherrington from London and Scott Kirkpatrick from IBM Laboratories simplified the model using the assumption that the strength of the interaction is exactly the same (but can still differ in one property - ferromagnetic or antiferromagnetic). The researchers hoped that this assumption, even if less realistic, would simplify the problem into a solution. Unfortunately, the system was still no less complex than the previous one and attempts to prove the existence of the spin-glass in this model failed. This is where Giorgio Frisi comes into the picture. The theoretical physicist solved the Sherrington-Kirkpatrick model and showed that every state with minimum energy is stable enough. The stability arises because the transition between one local minimum and another requires a large investment of energy and a large reversal of spins in the system.
Spin-glass and optimization problems
Despite the little that was known, the spin-glass phase helped a lot in understanding biological systems, neural networks and mathematical problems from computer science. The connection between the four systems is found in the enormous number of degrees of freedom. Their complexity creates a wide number of possible arrangements and makes it difficult for researchers to predict the state the system will find as a function of time. The first use of spin-glass was actually observed in optimization problems from computer science. The first parallel appeared in the "salesman" problem, a well-known optimization problem that seeks the shortest route through a finite number of destinations. The naive approach to solving the problem is to measure the lengths of the existing routes and choose the shortest route from the list, but as the number of stops increases, the number of routes increases exponentially. The shortest path problem is a perfect analogy to spin-glass: the targets are parallel to the spins, the lengths of the path are equal to the strength of the connections between the spins and the shortest length is equal to the minimum energy that the physical system chooses to be at. In other words, every time nature creates glass it solves an optimization problem! (I'll note that this is usually a local solution, if you want to search for the global minimum, you have to slowly heat and cool the system. Every time the system gets stuck in a stable state, you heat it up a little and cool it down slowly in the hope that it settles down to a state with lower energy). Many algorithms will have difficulty finding the global minimum in the system, but locally the solution is within reach. In line with this approach, in the XNUMXs researchers at IBM developed an algorithm based on Frisee's solution to find a local solution to optimization problems. For example, in the salesman problem, the algorithm will draw a very short route, one that will only get longer if the salesman decides to slightly deviate from his route, but it will not necessarily be the shortest route that exists on the map.
Spin-glass and biological systems
The connection of spin-glass to biology began in the late eighties and early nineties. Researcher John Hofield of the California Institute of Technology found many similarities between neural networks and spin-glass. Neurons can be broadly found in two states - on or off, just like spin measured on a single axis. The strength of the connection between neurons is a free parameter similar to the strength of the connections between the spins in the spin-glass phase. The main difference is that the connections in neurons change over time and in spin glass the connection is given and fixed. If the neuron networks are similar to spin-glass, the question arises what is the equivalent of the physical state with minimal energy? The accepted hypothesis today is that the stable structure of the spin-glass is analogous to the memory stored in networks. Another and surprising connection to spin glass is found in evolutionary processes of biological systems. One of the central questions in the field concerns the formation of the DNA molecule from amino acids. The chemical pathway from amino acids to molecules that carry information is not yet resolved, but it is possible to build mathematical models that describe a preference for complex systems with a lot of information. The amount of information in a polymer depends on how complex it is and how many states exist that create a similar pattern. It turns out that such patterns can be formed if one takes into account a mathematics similar to that of spin-glass.
And what about climate? The Nobel Prize in Physics was awarded to Prizi for his scientific contribution in understanding complex systems alongside climate researchers. The prize committee decided to focus on glass spin because this model is able to explain many phenomena outside the physics of materials. Climate is not directly related to Frisian, but statistical predictions of complex systems with lots of degrees of freedom belong in one category, along with climate science.

One response
Excellent! Thank you Noam.